题目内容
(21)已知 (I)求![]() 的解析式;
的解析式;
(II)是否存在实数![]() 使得方程
使得方程![]() 在区间
在区间![]() 内有且只有两个不等的实数根?若存在,求出
内有且只有两个不等的实数根?若存在,求出![]() 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。
本小题主要考查函数的单调性、极值等基本知识,考查运用导数研究函数的性质的方法,考查函数与方程、数形结合等数学思想方法和分析问题、解决问题的能力。
(I)解:![]()
![]() 是二次函数,且
是二次函数,且![]() 的解集是
的解集是![]()
![]() 可设
可设![]()
![]() 在区间
在区间![]() 上的最大值是
上的最大值是![]()
由已知,得![]()
![]()
(II)方程![]() 等价于方程
等价于方程![]()
设![]()
则![]()
当![]() 时,
时,![]() 是减函数;
是减函数;
当![]() 时,
时,![]() 是增函数。
是增函数。
![]()
![]() 方程
方程![]() 在区间
在区间![]() 内分别有惟一实数根,而在区间
内分别有惟一实数根,而在区间![]()
![]() 内没有实数根,
内没有实数根,
所以存在惟一的自然数![]() 使得方程
使得方程![]() 在区间
在区间![]() 内有且只有两个不同的实数根。
内有且只有两个不同的实数根。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
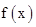 是二次函数,不等式
是二次函数,不等式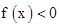 的解集是(0,5),且f(x)在区间[-1,4]上的最大值是12.
的解集是(0,5),且f(x)在区间[-1,4]上的最大值是12.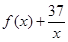 =0在区间(m,m+1)内有且只有两个不等的实数根?若存在,求出所有m的值;若不存在,请说明理由.
=0在区间(m,m+1)内有且只有两个不等的实数根?若存在,求出所有m的值;若不存在,请说明理由. 是二次函数,方程
是二次函数,方程 有两相等实根,且
有两相等实根,且
 的解析式.
的解析式. 所围成的图形的面积.
所围成的图形的面积.