题目内容
设函数f(x)=ln(1+x),g(x)=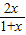 (x>0),数列{an}满足:a1=
(x>0),数列{an}满足:a1= ,an+1=g(an)(n∈N).
,an+1=g(an)(n∈N).(Ⅰ)当x>-1时,比较x与f(x)的大小;
(Ⅱ)求数列{an}的通项公式;
(Ⅲ)求证:a1+a2+…+an>ln
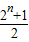 .
.
【答案】分析:(Ⅰ)构造函数F(x)=x-ln(1+x)利用导数求其最小值,从而判断得到x≥ln(1+x);
(Ⅱ)通过关系式an+1=g(an)变形得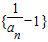 是一等比数列,并求其通项,从而计算出数列{an}的通项公式;
是一等比数列,并求其通项,从而计算出数列{an}的通项公式;
(Ⅲ)由(Ⅰ)中x≥ln(1+x)知an>ln(an+1),而ln(an+1)=ln(2n+1)-ln(2n-1+1),然后利用累加法化简即可证明结论.
解答:解:(Ⅰ)当x>-1时,设F(x)=x-ln(1+x),∴F'(x)=1-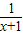 =
=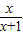 ,,令F'(x)=0 有x=0,
,,令F'(x)=0 有x=0,
当x∈(-1,0),F'(x)<0,F(x)单调递减;当x∈(0,+∞),F'(x)>0,F(x)单调递增.
∴F(x)的最小值为F(0)=0∴x≥ln(1+x);
(Ⅱ)∵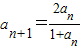 ,∴
,∴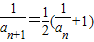 ,∴
,∴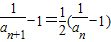 ,
,
∴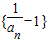 为首项是1、公比为
为首项是1、公比为 的等比数列.∴
的等比数列.∴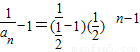 =
=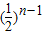 ,∴
,∴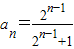 ;
;
(Ⅲ)∵an>0,由(Ⅰ)知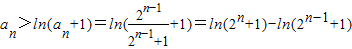 ,
,
∴a1+a2+…+an>[ln(21+1)-ln(2+1)+…+ln(2n+1)-ln(2n-1+1)]
=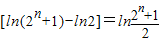 ,即证.
,即证.
点评:此题考查函数的导数应用,及数列求和中裂项相消法的运用.
(Ⅱ)通过关系式an+1=g(an)变形得
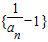 是一等比数列,并求其通项,从而计算出数列{an}的通项公式;
是一等比数列,并求其通项,从而计算出数列{an}的通项公式;(Ⅲ)由(Ⅰ)中x≥ln(1+x)知an>ln(an+1),而ln(an+1)=ln(2n+1)-ln(2n-1+1),然后利用累加法化简即可证明结论.
解答:解:(Ⅰ)当x>-1时,设F(x)=x-ln(1+x),∴F'(x)=1-
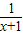 =
=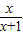 ,,令F'(x)=0 有x=0,
,,令F'(x)=0 有x=0,当x∈(-1,0),F'(x)<0,F(x)单调递减;当x∈(0,+∞),F'(x)>0,F(x)单调递增.
∴F(x)的最小值为F(0)=0∴x≥ln(1+x);
(Ⅱ)∵
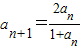 ,∴
,∴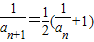 ,∴
,∴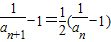 ,
,∴
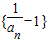 为首项是1、公比为
为首项是1、公比为 的等比数列.∴
的等比数列.∴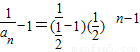 =
=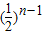 ,∴
,∴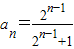 ;
;(Ⅲ)∵an>0,由(Ⅰ)知
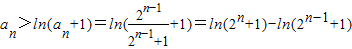 ,
,∴a1+a2+…+an>[ln(21+1)-ln(2+1)+…+ln(2n+1)-ln(2n-1+1)]
=
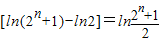 ,即证.
,即证.点评:此题考查函数的导数应用,及数列求和中裂项相消法的运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目