题目内容
在北纬60°的纬线圈上有A、B两地,它们在纬度圈上所对应的劣弧长等于
(R为地球半径),则A、B两地的球面距离是 ( )
| πR |
| 2 |
| A.2R | B.R | C.
| D.
|
北纬60°圈所在圆的半径为
,它们在纬度圈上所对应的劣弧长等于
(R为地球半径),
=θ×
(θ是A、B两地在北纬60°圈上对应的圆心角),
故 θ=
,∴线段AB=
×
=
,
设地球的中心为O,则△AOB中,由余弦定理得
=R2+R2-2R2cos∠AOB,
∴cos∠AOB=
,∠AOB=
,A、B这两地的球面距离是
,
故选D.
| R |
| 2 |
| πR |
| 2 |
| πR |
| 2 |
| R |
| 2 |
故 θ=
| π |
| 2 |
| 2 |
| R |
| 2 |
| ||
| 2 |
设地球的中心为O,则△AOB中,由余弦定理得
| 2R2 |
| 4 |
∴cos∠AOB=
| ||
| 2 |
| π |
| 3 |
| πR |
| 3 |
故选D.

练习册系列答案
相关题目
 (R为地球半径),则A、B两地的球面距离是 ( )
(R为地球半径),则A、B两地的球面距离是 ( ) R
R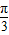 R
R