题目内容
设![]() =
=![]() ,其中a,b
,其中a,b![]() R,ab
R,ab![]() 0,若
0,若![]() 对一切则x
对一切则x![]() R恒成立,则
R恒成立,则
①![]() [
[
②![]() <
<![]()
③![]() 既不是奇函数也不是偶函数
既不是奇函数也不是偶函数
④![]() 的单调递增区间是
的单调递增区间是![]()
⑤存在经过点(a,b)的直线与函数的图![]() 像不相交
像不相交
以上结论正确的是 (写出所有正确结论的编号).
①③【命题意图】本题考查辅助角公式的应用,考查基本不等式,考查三角函数求值,考查三角函数的单调性以及三角函数的图像.
【解析】![]() ,又
,又![]() ,由题意
,由题意![]() 对一切则x
对一切则x![]() R恒成立,则
R恒成立,则![]() 对一切则x
对一切则x![]() R恒成立,即
R恒成立,即![]() ,
,![]() 恒成立,而
恒成立,而![]() ,所以
,所以![]() ,此时
,此时![]() .所以
.所以![]() .
.
①![]() ,故①正确;
,故①正确;
②![]() ,
,
![]() ,
,
所以![]() <
<![]() ,②错误;
,②错误;
③![]() ,所以③正确;
,所以③正确;
④由①知![]() ,
,![]() ,
,
由![]() 知
知![]() ,所以③不正确;
,所以③不正确;
⑤由①知![]() ,要经过点(a,b)的直线与函数的图
,要经过点(a,b)的直线与函数的图![]() 像不相交,则此直线与横轴平行,又
像不相交,则此直线与横轴平行,又![]() 的振幅为
的振幅为![]() ,所以直线必与
,所以直线必与![]() 图像有交点.⑤不正确.
图像有交点.⑤不正确.

练习册系列答案
相关题目
 =
= ,其中a,b
,其中a,b R,ab
R,ab 0,若
0,若 对一切则x
对一切则x
 <
<

 (其中a,b
(其中a,b R, i为虚数单位),则
R, i为虚数单位),则 0
0 0,6 =
0 (D) a
0,6 =
0 (D) a 0,b
0,b 0
0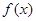 =
=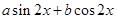 ,其中a,b
,其中a,b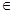 R,ab
R,ab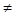 0,若
0,若 对一切则x
对一切则x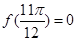 ;②
;②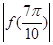 <
<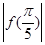 ;③
;③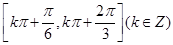 ;⑤存
;⑤存