题目内容
已知函数f(x)=ax2+(2b+3)x和函数g(x)=3x-c,其中a2-(b+c)a+bc>0且a+b+c=0.(1)求证:f(x)的图象与g(x)的图象总有两个不同的公共点;
(2)设f(x)的图象与g(x)的图象的两个公共点之间的距离为l,试求l的取值范围.
(1)证明:假设a=0,则bc>0,即b、c同号,
又a+b+c=0![]() b+c=0,这与b、c同号矛盾,所以a≠0.?
b+c=0,这与b、c同号矛盾,所以a≠0.?
由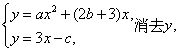
得ax2+2bx+c=0.?
所以Δ=4b2![]()
因为![]()
所以方程ax2+2bx+c=0总有两个不相等的实根,
即f(x)的图象与g(x)的图象总有两个不同的公共点.?
(2)解析:由a2-(b+c)a+bc>0且b=-(a+c),
所以![]()
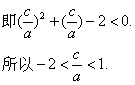
设f(x)的图象与g(x)的图象的两个交点为A(x1,y1)、B(x2,y2),?
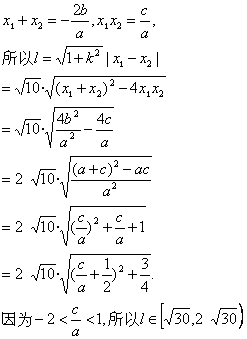

练习册系列答案
相关题目
已知函数f(x)=a-
,若f(x)为奇函数,则a=( )
| 1 |
| 2x+1 |
A、
| ||
| B、2 | ||
C、
| ||
| D、3 |