题目内容
已知正项等比数列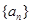 满足:
满足: ,若数列中存在两项
,若数列中存在两项 使得
使得 ,
,
则 的最小值为( )
的最小值为( )
| A.9 | B. | C. | D. |
D
解析试题分析:利用等比数列的知识求出m与n的关系,在利用基本不等式求解出最值. 即
即 .又因为
.又因为
 所以
所以 .故答案为D
.故答案为D
考点:等比数列、基本不等式

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
已知等比数列 中,
中, ,且
,且 ,则
,则 的值为( )
的值为( )
| A.4 | B.-4 | C.±4 | D.± |
在各项都为正数的等比数列 中,首项为3,前3项和为21,则
中,首项为3,前3项和为21,则 等于( )
等于( )
| A.15 | B.12 | C.9 | D.6 |
已知正项等比数列 满足
满足 。若存在两项
。若存在两项 使得
使得 ,则
,则 的最小值为( )
的最小值为( )
A. | B. | C. | D. |
已知等比数列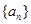 的公比
的公比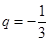 ,则
,则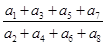 等于( )
等于( )
A.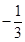 | B.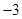 | C.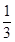 | D.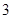 |
已知各项均为正数的等比数列 满足
满足 ,则
,则 的值为( )
的值为( )
| A.4 | B.2 | C.1或4 | D.1 |
在等比数列{ }中,若对n∈N*,都有
}中,若对n∈N*,都有 …
… ,则
,则 等于( )
等于( )
A. | B. | C. | D. |
 为等比数列,
为等比数列, ,则
,则 ( )
( )
A. | B.24 | C. | D.48 |
已知实数a,b,c,d成等比数列,且函数y=ln(x+2)-x,当x=b时取到极大值c,则ad等于( ).
| A.1 | B.0 | C.-1 | D.2 |