题目内容
已知函数f(x)=2x2+mx-1,集合A={x|log2(x+2)≥log2(x2+x+1)},B={x|32x8-1≤1}.
(1)设f(x)≤0的解集为C,若C⊆(A∪B),求m的取值范围;
(2)当m∈A,x∈B时,求证:|f(x)|≤ .
.
解:由题意log2(x+2)≥log2(x2+x+1),
得x+2≥x2+x+1>0,
解得-1≤x≤1;
由32x8-1≤1得x2≤
解得- ≤x≤
≤x≤ .
.
∴A=[-1,1],B=[- ,
, ],
],
∴A∪B=[-1,1].
(1)∵C={x|2x2+mx-1≤0}且C⊆(A∪B),
∴不等式2x2+mx-1≤0的解集是[-1,1]的子集.
∵△=m2+8>0,
∴只要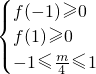 即可,解得-1≤m≤1.
即可,解得-1≤m≤1.
∴m的取值范围为[-1,1].
(2)∵m∈A,x∈B,∴|m|≤1,x2≤ .
.
∴|f(x)|=|2x2-1+mx|≤|2x2-1|+|mx|
≤-(2x2-1)+|x|
=-2(|x|- )2+
)2+ ≤
≤ .
.
分析:(1)由题意先化简集合A,B,再根据C⊆(A∪B),得到不等式2x2+mx-1≤0的解集是[-1,1]的子集.利用二次方程根的方布得出关于m的不等关系,从而求出m的取值范围;
(2)利用绝对值不等式的性质得出|f(x)|=|2x2-1+mx|≤|2x2-1|+|mx|≤-(2x2-1)+|x|再结合二次函数的性质即可得到证明.
点评:本小题主要考查函数单调性的应用、二次函数的性质、不等式的解法、交、并、补集的混合运算等基础知识,考查运算求解能力,考查转化思想.属于基础题.
得x+2≥x2+x+1>0,
解得-1≤x≤1;
由32x8-1≤1得x2≤

解得-
 ≤x≤
≤x≤ .
.∴A=[-1,1],B=[-
 ,
, ],
],∴A∪B=[-1,1].
(1)∵C={x|2x2+mx-1≤0}且C⊆(A∪B),
∴不等式2x2+mx-1≤0的解集是[-1,1]的子集.
∵△=m2+8>0,
∴只要
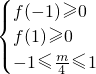 即可,解得-1≤m≤1.
即可,解得-1≤m≤1.∴m的取值范围为[-1,1].
(2)∵m∈A,x∈B,∴|m|≤1,x2≤
 .
.∴|f(x)|=|2x2-1+mx|≤|2x2-1|+|mx|
≤-(2x2-1)+|x|
=-2(|x|-
 )2+
)2+ ≤
≤ .
.分析:(1)由题意先化简集合A,B,再根据C⊆(A∪B),得到不等式2x2+mx-1≤0的解集是[-1,1]的子集.利用二次方程根的方布得出关于m的不等关系,从而求出m的取值范围;
(2)利用绝对值不等式的性质得出|f(x)|=|2x2-1+mx|≤|2x2-1|+|mx|≤-(2x2-1)+|x|再结合二次函数的性质即可得到证明.
点评:本小题主要考查函数单调性的应用、二次函数的性质、不等式的解法、交、并、补集的混合运算等基础知识,考查运算求解能力,考查转化思想.属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目