题目内容
设z=kx+y,其中实数x、y满足X≥2,x-2y+4≥0,2x-y-4≤0若z的最大值为12, 则实数k=________ .
【答案】2
【解析】次不等式表示的平面区域如图4所示y=-kx+z 。当k>0时,直线![]() :
:![]() 平移到A点时目标函数取最大值,即当4k+4=12 所以K=2 ,当K<0时 ,直线:
平移到A点时目标函数取最大值,即当4k+4=12 所以K=2 ,当K<0时 ,直线:![]()
平移到A或B点是目标函数取最大值,可知k取值是大于零,所以不满足,所以k=2,所以填2

【考点定位】此题考查线性规划知识点,把不等式组所表示的平面区域表示出来,然后对K进行分类讨论即可解决

练习册系列答案
相关题目
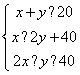 若z的最大值为12,则实数k= .
若z的最大值为12,则实数k= .