题目内容
已知函数 ,当
,当 时,给出下列几个结论:
时,给出下列几个结论:
①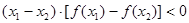 ;②
;②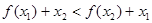 ;③
;③ ;
;
④当 时,
时, .
.
其中正确的是 (将所有你认为正确的序号填在横线上).
③④
解析试题分析:因为 ,所以
,所以 ,可知(0,
,可知(0, )递减,(
)递减,( ,+∞)递增,故①错误;令
,+∞)递增,故①错误;令 ,所以
,所以 ,可知
,可知 在(0,1)上递减,(1,+∞)上递增,故②错;令
在(0,1)上递减,(1,+∞)上递增,故②错;令 ,所以h(x)在(0,+∞)上递增,所以
,所以h(x)在(0,+∞)上递增,所以
 ,故③正确;当
,故③正确;当 时,可知
时,可知 ,又因为f(x)在(
,又因为f(x)在( ,+∞)递增, 设
,+∞)递增, 设

 ,又因为f(x)在(
,又因为f(x)在( ,+∞)递增,所以
,+∞)递增,所以 时,
时, 即
即 ,所以
,所以 时,
时, ,故
,故 为增函数,所以
为增函数,所以 ,所以
,所以
 ,故④正确.
,故④正确.
考点:导函数在不等式中的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 与曲线
与曲线 有公共点,则实数
有公共点,则实数 的取值范围是 .
的取值范围是 .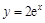 相切,则实数k = .
相切,则实数k = . 在区间
在区间 上是减函数,那么
上是减函数,那么 的最大值为 .
的最大值为 .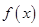 的导函数为
的导函数为 ,若
,若 ,则
,则 .
. ,若
,若 ,则
,则 ;
;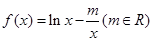 在区间
在区间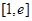 上取得最小值4,则
上取得最小值4,则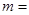 ___________.
___________.