题目内容
若n为函数f（x）=|x-3|+|x-6|+|x-12|的最小值，则二项式(x2+
)n的展开式中的常数项是（ ）
| 2 |
| x |
| A．12 | B．240 | C．2688 | D．5376 |
据绝对值的几何意义知，
f（x）=|x-3|+|x-6|+|x-12|表示数轴上的点到3，；6；12的距离的和
故当x=6时，距离最小
故n=9
∴(x2+
)n=(x2+
)9展开式的通项Tr+1=2rC9rx18-3r
令18-3r=0得r=6
展开式的常数项为26C96=5376
故选D
f（x）=|x-3|+|x-6|+|x-12|表示数轴上的点到3，；6；12的距离的和
故当x=6时，距离最小
故n=9
∴(x2+
| 2 |
| x |
| 2 |
| x |
令18-3r=0得r=6
展开式的常数项为26C96=5376
故选D
练习册系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
若n为函数f（x）=|x-3|+|x-6|+|x-12|的最小值，则二项式(x2+
)n的展开式中的常数项是（ ）
| 2 |
| x |
| A、12 | B、240 |
| C、2688 | D、5376 |
)n的展开式中的常数项是
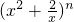的展开式中的常数项是
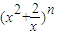的展开式中的常数项是（ ）