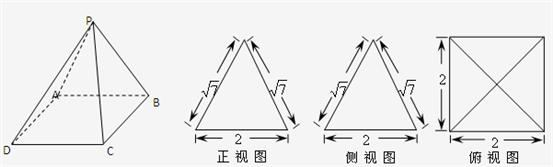
题目内容
一个多面体的直观图和三视图如图所示,其中![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,![]() 是
是![]() 上的一动点.
上的一动点.
(Ⅰ)求该几何体的体积与表面积;
(Ⅱ)求证:![]() ⊥
⊥![]() ;
;
(Ⅲ)当![]() 时,在棱
时,在棱![]() 上确定一点
上确定一点![]() ,使得
,使得![]() //平面
//平面![]() ,并给出证明.
,并给出证明.
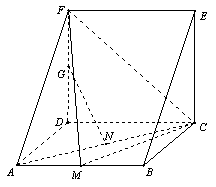
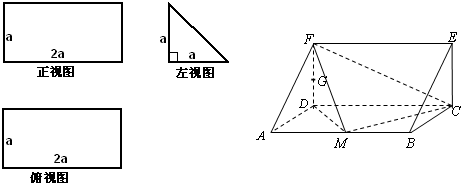
 |  | ||
(Ⅰ)由三视图可知直观图为直三棱柱,
底面![]() 中
中![]() ⊥
⊥![]() ,
,![]() ,
,
该几何体的体积为![]() ,表面积为
,表面积为![]() . …4分
. …4分
(Ⅱ)证明:连接![]() ,可知
,可知![]() ,
,![]() ,
,![]() 共线,且
共线,且![]() ⊥
⊥![]() .
.
又![]()
![]() ⊥
⊥![]()
![]() ⊥
⊥![]() ,
, ![]() ,
,
![]()
![]() ⊥面
⊥面![]() . 又
. 又![]()
![]()
![]() 面
面![]()
![]()
![]() ⊥
⊥![]() .
.
又![]()
![]() ,
,
![]()
![]() ⊥面
⊥面![]() 又
又![]() ,
,
![]()
![]() ⊥
⊥![]() . . ……………………. . …………….8分
. . ……………………. . …………….8分
(Ⅲ)点![]() 与点
与点![]() 重合时,
重合时,![]() ∥面
∥面![]() . . …………………….…………….10分
. . …………………….…………….10分
证明:取![]() 中点
中点![]() ,连接
,连接![]() .
.
![]()
![]() 是
是![]() 的中点
的中点 ![]()
![]()
![]()
![]()
![]() .
. ![]()
![]() 是
是![]() 的中点
的中点 ![]()
![]()
![]()
![]()
![]() .
.
![]()
![]() //
//![]() 且
且 ![]() =
=![]()
![]() 四边形
四边形![]() 是平行四边形.
是平行四边形.
![]()
![]() //
// ![]() . 又
. 又![]()
![]() 面
面![]() ,
, ![]()
![]() 面
面![]() ,
,
![]()
![]() //面
//面![]() 即GP//面
即GP//面![]() . . …………….…….…………….……….13分
. . …………….…….…………….……….13分

练习册系列答案
相关题目
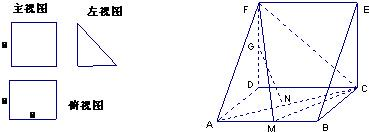 一个多面体的直观图和三视图如图所示,其中M、N分别是AB、AC的中点,G是DF上的一动点.
一个多面体的直观图和三视图如图所示,其中M、N分别是AB、AC的中点,G是DF上的一动点.