题目内容
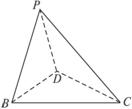
已知在平面四边形ABCD中,AD∥BC,AD=AB=1,∠BCD=45°,∠BAD=90°,将△ABD沿对角线BD折起到△PBD的位置(如图所示),使平面PBD⊥平面BCD.(1)求证:CD⊥PB;
(2)求二面角PBCD的平面角的正切值.
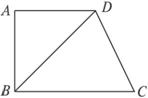
(1)证明:因为∠BAD=90°,AD=AB,所以∠ADB=∠ABD=45°,∠BDC=90°,即BD⊥DC.
又平面PBD⊥平面BCD,CD![]() 平面BCD,所以CD⊥平面PBD.
平面BCD,所以CD⊥平面PBD.
又PB![]() 平面PBD,所以CD⊥PB.
平面PBD,所以CD⊥PB.
(2)解:过点P作PE⊥BD于E.因为平面PBD⊥平面BCD,所以PE⊥平面BCD.过E作EF⊥BC于F,连结PF,则PE⊥PF,BC⊥平面PEF,所以BC⊥PF,∠PFE为二面角PBCD的平面角.
又PB=PD=1,所以PE=BE=![]() ,EF=
,EF=![]() BE=
BE=![]() .
.
在Rt△PEF中,∠PEF=90°,tan∠PFE=![]() ,故二面角PBCD的平面角的正切值是
,故二面角PBCD的平面角的正切值是![]() .
.

练习册系列答案
相关题目
 (2011•顺义区一模)如图,已知在空间四边形ABCD中,AB=AC=DB=DC,E为BC的中点.
(2011•顺义区一模)如图,已知在空间四边形ABCD中,AB=AC=DB=DC,E为BC的中点. 如图甲,在平面四边形ABCD中,已知∠A=45°,∠C=90°,AB=BD=2CD,现将四边形ABCD沿BD折起,使平面ABD⊥平面BDC(如图乙),设点E为棱AD的中点.
如图甲,在平面四边形ABCD中,已知∠A=45°,∠C=90°,AB=BD=2CD,现将四边形ABCD沿BD折起,使平面ABD⊥平面BDC(如图乙),设点E为棱AD的中点. 如图,已知在空间四边形ABCD中,AB=AC=DB=DC,E为BC的中点.
如图,已知在空间四边形ABCD中,AB=AC=DB=DC,E为BC的中点.