题目内容
如图,已知矩形油画的长为a,宽为b.在该矩形油画的四边镶金箔,四个角(图中斜线区域)装饰矩形木雕,制成一幅矩形壁画.设壁画的左右两边金箔的宽为x,上下两边金箔的宽为y,壁画的总面积为S.(1)用x,y,a,b表示S;
(2)若S为定值,为节约金箔用量,应使四个矩形木雕的总面积最大.求四个矩形木雕总面积的最大值及对应的x,y的值.

【答案】分析:(1)直接根据图形由9个小矩形构成,分别求出面积求和即可;
(2)依题意,即求4xy的最大值,根据基本不等式可得S≥ +4xy+ab,当且仅当bx=ay时等号成立,令t=
+4xy+ab,当且仅当bx=ay时等号成立,令t= ,则t>0,上述不等式可以为4t2+4
,则t>0,上述不等式可以为4t2+4 t+ab-S≤0,解不等式可求出四个矩形木雕总面积的最大值及对应的x,y的值.
t+ab-S≤0,解不等式可求出四个矩形木雕总面积的最大值及对应的x,y的值.
解答:解:(1)壁画由9个小矩形构成,其面积为9个矩形的面积和
∴壁画的总面积为S=2bx+2ay+4xy+ab,x,y>0
(2)依题意,即求4xy的最大值
因为x,y>0,所以2bx+2ay≥2 ,从而S≥4
,从而S≥4 +4xy+ab,当且仅当bx=ay时等号成立
+4xy+ab,当且仅当bx=ay时等号成立
令t= ,则t>0,上述不等式可以为4t2+4
,则t>0,上述不等式可以为4t2+4 t+ab-S≤0
t+ab-S≤0
解得 ≤t≤
≤t≤
因为t>0,所以t≤ ,从而xy≤
,从而xy≤
由
解得 (舍去负值)
(舍去负值)
所以当x= ,y=
,y= 时,四个矩形木雕的总面积最大,最大值为ab+S-2
时,四个矩形木雕的总面积最大,最大值为ab+S-2
点评:本题主要考查了基本不等式在最值问题中的应用,同时考查了计算能力,解题的关键是解方程,属于中档题.
(2)依题意,即求4xy的最大值,根据基本不等式可得S≥
 +4xy+ab,当且仅当bx=ay时等号成立,令t=
+4xy+ab,当且仅当bx=ay时等号成立,令t= ,则t>0,上述不等式可以为4t2+4
,则t>0,上述不等式可以为4t2+4 t+ab-S≤0,解不等式可求出四个矩形木雕总面积的最大值及对应的x,y的值.
t+ab-S≤0,解不等式可求出四个矩形木雕总面积的最大值及对应的x,y的值.解答:解:(1)壁画由9个小矩形构成,其面积为9个矩形的面积和
∴壁画的总面积为S=2bx+2ay+4xy+ab,x,y>0
(2)依题意,即求4xy的最大值
因为x,y>0,所以2bx+2ay≥2
 ,从而S≥4
,从而S≥4 +4xy+ab,当且仅当bx=ay时等号成立
+4xy+ab,当且仅当bx=ay时等号成立令t=
 ,则t>0,上述不等式可以为4t2+4
,则t>0,上述不等式可以为4t2+4 t+ab-S≤0
t+ab-S≤0解得
 ≤t≤
≤t≤
因为t>0,所以t≤
 ,从而xy≤
,从而xy≤
由

解得
 (舍去负值)
(舍去负值)所以当x=
 ,y=
,y= 时,四个矩形木雕的总面积最大,最大值为ab+S-2
时,四个矩形木雕的总面积最大,最大值为ab+S-2
点评:本题主要考查了基本不等式在最值问题中的应用,同时考查了计算能力,解题的关键是解方程,属于中档题.

练习册系列答案
相关题目
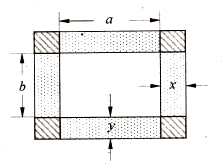 (2012•江苏二模)如图,已知矩形油画的长为a,宽为b.在该矩形油画的四边镶金箔,四个角(图中斜线区域)装饰矩形木雕,制成一幅矩形壁画.设壁画的左右两边金箔的宽为x,上下两边金箔的宽为y,壁画的总面积为S.
(2012•江苏二模)如图,已知矩形油画的长为a,宽为b.在该矩形油画的四边镶金箔,四个角(图中斜线区域)装饰矩形木雕,制成一幅矩形壁画.设壁画的左右两边金箔的宽为x,上下两边金箔的宽为y,壁画的总面积为S.