题目内容
![]()
![]() 如图5,在直角梯形ABCP中,AP//BC,AP
如图5,在直角梯形ABCP中,AP//BC,AP![]() AB,AB=BC=
AB,AB=BC=![]() ,D是AP的中点,E,F,G分别为PC、PD、CB的中点,将
,D是AP的中点,E,F,G分别为PC、PD、CB的中点,将![]() 沿CD折起,使得
沿CD折起,使得![]() 平面ABCD, 如图6.
平面ABCD, 如图6.
(Ⅰ)求证:AP//平面EFG;
(Ⅱ) 求二面角![]() 的大小;
的大小;
(Ⅲ)求三棱椎![]() 的体积.
的体积.
 | |||
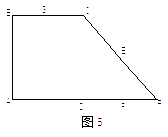 | |||
![]() ;
;![]()
解析:
(Ⅰ) 证明:方法一)连AC,BD交于O点,连GO,FO,EO.
∵E,F分别为PC,PD的中点,∴![]() //
//![]() ,同理
,同理![]() //
//![]() ,
, ![]() //
// ![]()
![]() 四边形EFOG是平行四边形,
四边形EFOG是平行四边形, ![]() 平面EFOG.
平面EFOG.
又在三角形PAC中,E,O分别为PC,AC的中点,![]() PA//EO
PA//EO
![]() 平面EFOG,PA
平面EFOG,PA![]() 平面EFOG,
平面EFOG,
![]() PA//平面EFOG,即PA//平面EFG.
PA//平面EFOG,即PA//平面EFG.
方法二) 连AC,BD交于O点,连GO,FO,EO.
∵E,F分别为PC,PD的中点,∴![]() //
//![]() ,同理
,同理![]() //
//![]()
又![]() //AB,
//AB,![]() //
//![]()
![]() 平面EFG//平面PAB,
平面EFG//平面PAB,
又PA![]() 平面PAB,
平面PAB,![]() 平面EFG. ……6分
平面EFG. ……6分
方法三)如图以D为原点,以![]()
 为方向向量建立空间直角坐标系
为方向向量建立空间直角坐标系![]() .
.
![]() 则有关点及向量的坐标为:
则有关点及向量的坐标为:
![]()
![]()
设平面EFG的法向量为![]()
 取
取![]() .
.
∵![]() ,
,
又![]() 平面EFG.
平面EFG.![]() AP//平面EFG.
AP//平面EFG.
(Ⅱ)由已知底面ABCD是正方形
![]()
![]() ,又∵
,又∵![]() 面ABCD
面ABCD ![]()
又![]()
![]() 平面PCD,
平面PCD,
![]() 向量
向量![]() 是平面PCD的一个法向量,
是平面PCD的一个法向量, ![]() =
=![]()
又由(Ⅰ)方法三)知平面EFG的法向量为![]()

结合图知二面角![]() 的平面角为
的平面角为![]()
(Ⅲ)![]()

练习册系列答案
相关题目
 本题(1)(2)(3)三个选答题,每小题5分,请考生任选1题作答,如果多做,则按所做的前1题计分.
本题(1)(2)(3)三个选答题,每小题5分,请考生任选1题作答,如果多做,则按所做的前1题计分. ,点E,F分别为线段AB,CD的中点,则EF= .
,点E,F分别为线段AB,CD的中点,则EF= .
 )
) 中,曲线
中,曲线 的交点的极坐标为
.
的交点的极坐标为
.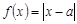 .若不等式
.若不等式 ,则实数
,则实数 的值为
.
的值为
. 本题(1)(2)(3)三个选答题,每小题5分,请考生任选1题作答,如果多做,则按所做的前1题计分.
本题(1)(2)(3)三个选答题,每小题5分,请考生任选1题作答,如果多做,则按所做的前1题计分. ,点E,F分别为线段AB,CD的中点,则EF=________.
,点E,F分别为线段AB,CD的中点,则EF=________.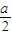 ,点E,F分别为线段AB,CD的中点,则EF= .
,点E,F分别为线段AB,CD的中点,则EF= .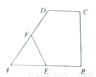
 CB⊥AB,AB=AD=
CB⊥AB,AB=AD= a,CD=
a,CD= ,点E,F分别为线段AB,CD的中点,则EF=" " .
,点E,F分别为线段AB,CD的中点,则EF=" " .
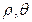 )
) 中,曲线
中,曲线 的交点的极坐标为 .
的交点的极坐标为 . .若不等式
.若不等式 ,则实数
,则实数 的值为 .
的值为 .