题目内容
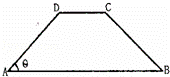
如图,在等腰梯形ABCD中,AB∥CD,且AB=2AD,设∠DAB=θ,θ∈(0,![]() ),以A,B为焦点且过点D的双曲线的离心率为e1,以C,D为焦点且过点A的椭圆的离心率为e2,则( )
),以A,B为焦点且过点D的双曲线的离心率为e1,以C,D为焦点且过点A的椭圆的离心率为e2,则( )
|
| A. | 随着角度θ的增大,e1增大,e1e2为定值 |
|
| B. | 随着角度θ的增大,e1减小,e1e2为定值 |
|
| C. | 随着角度θ的增大,e1增大,e1e2也增大 |
|
| D. | 随着角度θ的增大,e1减小,e1e2也减小 |
考点:
椭圆的简单性质.
专题:
计算题;压轴题.
分析:
连接BD、AC,假设AD=t,根据余弦定理表示出BD,进而根据双曲线的性质可得到a的值,再由AB=2c,e=![]() 可表示出e1=
可表示出e1=![]() ,最后根据余弦函数的单调性可判断e1的单调性;同样表示出椭圆中的c'和a'表示出e2的关系式,最后令e1、e2相乘即可得到e1e2的关系.
,最后根据余弦函数的单调性可判断e1的单调性;同样表示出椭圆中的c'和a'表示出e2的关系式,最后令e1、e2相乘即可得到e1e2的关系.
解答:
解:连接BD,AC设AD=t
则BD=![]() =
=![]()
∴双曲线中a=![]()
e1=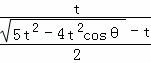
∵y=cosθ在(0,![]() )上单调减,进而可知当θ增大时,y=
)上单调减,进而可知当θ增大时,y=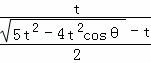 =
=![]() 减小,即e1减小
减小,即e1减小
∵AC=BD
∴椭圆中CD=2t(1﹣cosθ)=2c∴c'=t(1﹣cosθ)
AC+AD=![]() +t,∴a'=
+t,∴a'=![]() (
(![]() +t)
+t)
e2=![]() =
=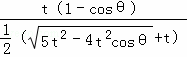
∴e1e2=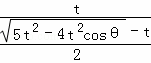 ×
×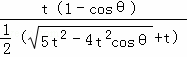 =1
=1
故选B.
点评:
本题主要考查椭圆和双曲线的离心率的表示,考查考生对圆锥曲线的性质的应用,圆锥曲线是高考的重点每年必考,平时要注意基础知识的积累和练习.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
 如图,在等腰梯形ABCD中,AB∥DC,AB=4,CD=2,等腰梯形的高为3,O为AB中点,PO⊥平面ABCD,垂足为O,PO=2,EA∥PO.
如图,在等腰梯形ABCD中,AB∥DC,AB=4,CD=2,等腰梯形的高为3,O为AB中点,PO⊥平面ABCD,垂足为O,PO=2,EA∥PO.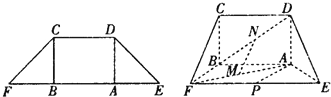 如图,在等腰梯形CDEF中,CB、DA是梯形的高,AE=BF=2,AB=2
如图,在等腰梯形CDEF中,CB、DA是梯形的高,AE=BF=2,AB=2 选修4-1;几何证明选讲.
选修4-1;几何证明选讲. (2012•河北模拟)如图,在等腰梯形ABCD中,CD=2,AB=4,AD=BC=
(2012•河北模拟)如图,在等腰梯形ABCD中,CD=2,AB=4,AD=BC=