题目内容
4.已知长方体ABCD-A1B1C1D1中,B1C,C1D与底面ABCD所成的角分别为60°和45°,则异面直线B1C和C1D所成角的余弦值为( )| A. | $\frac{\sqrt{6}}{4}$ | B. | $\frac{1}{4}$ | C. | $\frac{\sqrt{2}}{6}$ | D. | $\frac{\sqrt{3}}{6}$ |
分析 利用长方体的性质、线面角的定义、异面直线所成的角的定义即可得出.
解答 解:如图所示: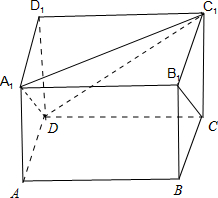
∵B1B⊥平面ABCD,∴∠BCB1是B1C与底面所成角,
∴∠BCB1=60°.
∵C1C⊥底面ABCD,∴∠CDC1是C1D与底面所成的角,
∴∠CDC1=45°.
连接A1D,A1C1,则A1D∥B1C.∴∠A1DC1或其补角为异面直线B1C与C1D所成的角.
不妨设BC=1,则CB1=DA1=2,BB1=CC1=$\sqrt{3}$=CD,
∴C1D=$\sqrt{6}$,A1C1=2.
在等腰△A1C1D中,cos∠A1DC1=$\frac{\sqrt{6}}{4}$.
故选:A.
点评 熟练掌握长方体的性质、线面角与异面直线所成的角的定义是解题的关键.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
15.已知函数f(x)的图象关于x=-1对称,且f(x)在(-1,+∞)上单调,若数列{an}是公差不为0的等差数列,且f(a50)=f(a51),则{an}的前100项的和为( )
| A. | -200 | B. | -100 | C. | -50 | D. | 0 |
12.执行如图所示的程序框图,输出的y等于( )


| A. | $\frac{1}{2}$ | B. | 0 | C. | -$\frac{1}{2}$ | D. | 1 |
16.执行如图所示的程序框图,若输入m=4,n=6,则输出a=( )


| A. | 4 | B. | 8 | C. | 12 | D. | 16 |