题目内容
已知函数f(x)=ax-lnx，x∈(0，e]，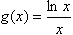
，其中e是自然常数，其近似值为2.71828，a∈R。
（1）当a=1时，求函数f(x)的极值；
（2）求证：在（1）的条件下，f(x)＞g(x)+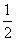
；
（3）是否存在实数a，使f(x)的最小值是3，若存在，求出a的值；若不存在，说明理由.
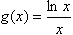，其中e是自然常数，其近似值为2.71828，a∈R。（1）当a=1时，求函数f(x)的极值；
（2）求证：在（1）的条件下，f(x)＞g(x)+
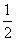；（3）是否存在实数a，使f(x)的最小值是3，若存在，求出a的值；若不存在，说明理由.
解：（1）f(x)=ax-lnx，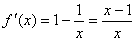
，
∴当x∈(0，1)时，
，此时f(x)单调递减；
当x∈(1，e)时，，此时f(x)单调递增，
∴f(x)的极小值为f（1）=1.
（2）f(x)的极小值为1，即f(x)在(0，e]上的最小值为1， ∴f(x)＞0，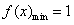
，
令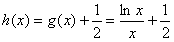
，
，
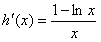当0＜x＜e时，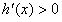
，h(x)在(0，e]上单调递增，
∴
，
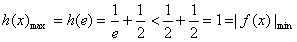∴在（1）的条件下，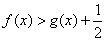
。
（3）假设存在实数，使f(x)=ax-lnx（x∈(0，e]）有最小值3，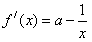
，
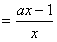①当a≤0时，f(x)在(0，e]上单调递减，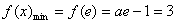
，
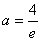（舍去），所以，此时f(x)无最小值；
②当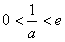
时，f(x)在
上单调递减，在
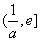上单调递增，
，
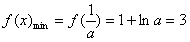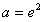，满足条件；
③当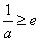
时，f(x)在(0，e]上单调递减，
，
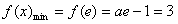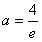（舍去），
所以，此时f(x)无最小值；
综上，存在实数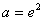
，使得当x∈(0，e]时，f(x)有最小值3。
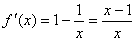，∴当x∈(0，1)时，
，此时f(x)单调递减；当x∈(1，e)时，
，此时f(x)单调递增，∴f(x)的极小值为f（1）=1.
（2）f(x)的极小值为1，即f(x)在(0，e]上的最小值为1， ∴f(x)＞0，
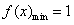，令
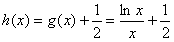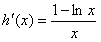，，当0＜x＜e时，
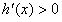，h(x)在(0，e]上单调递增，∴
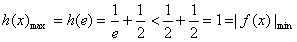，∴在（1）的条件下，
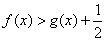。（3）假设存在实数，使f(x)=ax-lnx（x∈(0，e]）有最小值3，
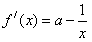
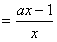，①当a≤0时，f(x)在(0，e]上单调递减，
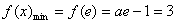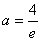，（舍去），所以，此时f(x)无最小值；②当
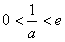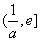时，f(x)在上单调递减，在上单调递增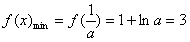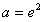，，，满足条件；③当
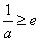时，f(x)在(0，e]上单调递减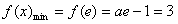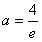，，（舍去），所以，此时f(x)无最小值；
综上，存在实数
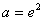，使得当x∈(0，e]时，f(x)有最小值3。 
练习册系列答案
阅读快车系列答案
相关题目
已知函数f(x)=a-
，若f（x）为奇函数，则a=（ ）
| 1 |
| 2x+1 |
A、
| ||
| B、2 | ||
C、
| ||
| D、3 |