题目内容
已知函数f(x)=sinωx-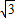 cosωx(ω>0)的图象与x轴的两个相邻交点的距离等于
cosωx(ω>0)的图象与x轴的两个相邻交点的距离等于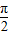 ,若将函数y=f(x)的图象向左平移
,若将函数y=f(x)的图象向左平移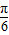 个单位得到函数y=g(x)的图象,则y=g(x)是减函数的区间为( )
个单位得到函数y=g(x)的图象,则y=g(x)是减函数的区间为( )A.
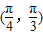
B.
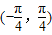
C.
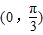
D.
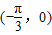
【答案】分析:由已知可求出函数f(x)的解析式,进而根据函数图象的平移变换法则得到函数y=g(x)的解析式,根据正弦函数的性质分析出函数的单调性后,比照四个答案即可得到结论.
解答:解:∵函数f(x)=sinωx-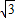 cosωx=2sin(ωx-
cosωx=2sin(ωx-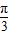 )
)
又∵函数f(x)=sinωx-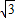 cosωx(ω>0)的图象与x轴的两个相邻交点的距离等于
cosωx(ω>0)的图象与x轴的两个相邻交点的距离等于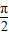 =
=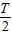
故函数的最小正周期T=π,
又∵ω>0
∴ω=2
故f(x)=2sin(2x-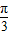 )
)
将函数y=f(x)的图象向左平移 个单位可得y=g(x)=2sin[2(x+
个单位可得y=g(x)=2sin[2(x+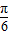 )-
)-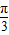 ]=2sin2x的图象
]=2sin2x的图象
令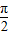 +2kπ≤2x≤
+2kπ≤2x≤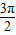 +2kπ,即
+2kπ,即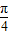 +kπ≤x≤
+kπ≤x≤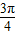 +kπ,k∈Z
+kπ,k∈Z
故函数y=g(x)的减区间为[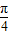 +kπ,
+kπ,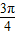 +kπ],k∈Z
+kπ],k∈Z
当k=0时,区间[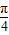 ,
,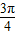 ]为函数的一个单调递减区间
]为函数的一个单调递减区间
又∵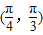 ⊆[
⊆[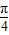 ,
,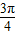 ]
]
故选A
点评:本题考查的知识点是函数y=Asin(ωx+φ)的图象变换,两角和与差的正弦函数,正弦函数的单调性,熟练掌握正弦型函数的图象性质及变换法则是解答本题的关键.
解答:解:∵函数f(x)=sinωx-
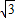 cosωx=2sin(ωx-
cosωx=2sin(ωx-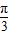 )
)又∵函数f(x)=sinωx-
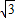 cosωx(ω>0)的图象与x轴的两个相邻交点的距离等于
cosωx(ω>0)的图象与x轴的两个相邻交点的距离等于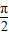 =
=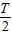
故函数的最小正周期T=π,
又∵ω>0
∴ω=2
故f(x)=2sin(2x-
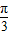 )
)将函数y=f(x)的图象向左平移
 个单位可得y=g(x)=2sin[2(x+
个单位可得y=g(x)=2sin[2(x+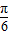 )-
)-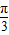 ]=2sin2x的图象
]=2sin2x的图象令
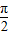 +2kπ≤2x≤
+2kπ≤2x≤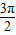 +2kπ,即
+2kπ,即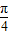 +kπ≤x≤
+kπ≤x≤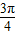 +kπ,k∈Z
+kπ,k∈Z故函数y=g(x)的减区间为[
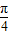 +kπ,
+kπ,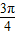 +kπ],k∈Z
+kπ],k∈Z当k=0时,区间[
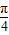 ,
,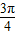 ]为函数的一个单调递减区间
]为函数的一个单调递减区间又∵
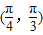 ⊆[
⊆[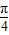 ,
,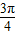 ]
]故选A
点评:本题考查的知识点是函数y=Asin(ωx+φ)的图象变换,两角和与差的正弦函数,正弦函数的单调性,熟练掌握正弦型函数的图象性质及变换法则是解答本题的关键.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
