题目内容
已知椭圆C: (a>b>0)的离心率为
(a>b>0)的离心率为 ,且椭圆C上一点与两个焦点F1,F2构成的三角形的周长为2
,且椭圆C上一点与两个焦点F1,F2构成的三角形的周长为2 +2.
+2.
(1)求椭圆C的方程;
(2)过右焦点F2作直线l 与椭圆C交于A,B两点,设 ,若
,若 ,求
,求 的取值范围.
的取值范围.
(1)  ; (2)
; (2) 
解析试题分析:(1)由题设知

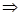 椭圆的标准方程为
椭圆的标准方程为
(2)因为当直线 的斜率不存在时,
的斜率不存在时, ,不适合题意,所以直线
,不适合题意,所以直线 的斜率存在,设为
的斜率存在,设为 ,直线
,直线 的方程为
的方程为 ,它与椭圆的两交点坐标
,它与椭圆的两交点坐标 ,则由
,则由 得
得
通过方程组 ,借助韦达定理,得到
,借助韦达定理,得到 ,结合
,结合 得到
得到 与
与 的关系式,并且可由
的关系式,并且可由 得到
得到 的取值范围;
的取值范围;
另一方面,因为
 由前述
由前述 的取值范围可使问题得到解决.
的取值范围可使问题得到解决.
试题解析:
解:(1)由题意知: ,且
,且 , 2分
, 2分
解得 , 3分
, 3分 椭圆
椭圆 的方程为
的方程为 . 4分
. 4分
(2)由题意得直线 的斜率存在,右焦点
的斜率存在,右焦点 ,可设直线
,可设直线 的方程为:
的方程为:
由 得
得
由题意
设 ,则
,则 6分
6分
由 得
得 7分
7分

 9分
9分
令 ,
, 在
在 上单调递增,
上单调递增,
可得

故 ,解得
,解得 2分
2分
= 13分
13分
即 的取值范围是
的取值范围是
练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
 ,斜率为2的直线l过点A(2,3).
,斜率为2的直线l过点A(2,3).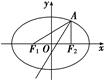
 的两个焦点分别为
的两个焦点分别为 和
和 ,离心率
,离心率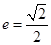 .
. (
(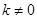 )与椭圆
)与椭圆 、
、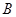 ,且线段
,且线段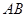
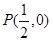 ,求实数
,求实数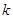 的取值范围.
的取值范围.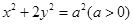 的一个顶点和两个焦点构成的三角形的面积为4.
的一个顶点和两个焦点构成的三角形的面积为4.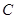 的方程;
的方程; 与椭圆
与椭圆 、
、 两点,试问,是否存在
两点,试问,是否存在 轴上的点
轴上的点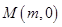 ,使得对任意的
,使得对任意的 ,
, 为定值,若存在,求出
为定值,若存在,求出 点的坐标,若不存在,说明理由.
点的坐标,若不存在,说明理由.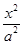 +
+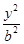 =1
=1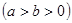 的离心率为
的离心率为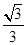 ,左焦点为F(-1,0),
,左焦点为F(-1,0),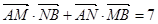 ,求直线L的方程;
,求直线L的方程;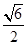 ?
? 与抛物线
与抛物线 (常数
(常数 )相交于不同的两点
)相交于不同的两点 、
、 ,且
,且 (
( 为定值),线段
为定值),线段 的中点为
的中点为 ,与直线
,与直线 平行的切线的切点为
平行的切线的切点为 (不与抛物线对称轴平行或重合且与抛物线只有一个公共点的直线称为抛物线的切线,这个公共点为切点).
(不与抛物线对称轴平行或重合且与抛物线只有一个公共点的直线称为抛物线的切线,这个公共点为切点).
 、
、 表示出
表示出 垂直于
垂直于 轴;
轴; 的面积,证明
的面积,证明 、
、 ,再作与
,再作与 、
、 ,小张马上写出了
,小张马上写出了 、
、 的面积,由此小张求出了直线
的面积,由此小张求出了直线 与抛物线围成的面积,你认为小张能做到吗?请你说出理由.
与抛物线围成的面积,你认为小张能做到吗?请你说出理由. 的中心为原点
的中心为原点 ,长轴在
,长轴在 轴上,离心率
轴上,离心率 ,又椭圆
,又椭圆 .
.
 轴的直线
轴的直线 与椭圆
与椭圆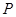 、
、 ,过
,过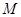 的圆,使椭圆
的圆,使椭圆 的面积
的面积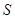 的最大值.
的最大值.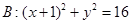 ,C为圆B上任意一点,求AC垂直平分线与线段BC的交点P的轨迹方程。
,C为圆B上任意一点,求AC垂直平分线与线段BC的交点P的轨迹方程。 .过点(m,0)作圆
.过点(m,0)作圆 的切线l交椭圆G于A,B两点.
的切线l交椭圆G于A,B两点. 表示为m的函数,并求
表示为m的函数,并求