题目内容
(本题满分12分)在数列{an}中,已知a =-20,a
=-20,a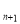 =a
=a +4(n∈
+4(n∈ ).
).
(1)求数列{an}的通项公式和前n项和An;
(2)若 (n∈
(n∈ ),求数列{bn}的前n项Sn.
),求数列{bn}的前n项Sn.
(1)  ,A
,A =
= (n∈
(n∈ );(2)
);(2)
【解析】
试题分析:(1)由a =-20,a
=-20,a =a
=a +4(n∈
+4(n∈ )确定数列
)确定数列 为等差数列,并确定其首项与公差,从而由等差数列的通项公式与前
为等差数列,并确定其首项与公差,从而由等差数列的通项公式与前 项和公式求得
项和公式求得 .
.
(2)由(1)的结果知:
所以可用拆项法求数列 的前
的前 项和.
项和.
试题解析:【解析】
(1)∵数列{an}满足a =a
=a +4(n∈
+4(n∈ ),∴数列{an}是以公差为4,以a
),∴数列{an}是以公差为4,以a =-20为首项的等差数列.
=-20为首项的等差数列.
故数列{an}的通项公式为a =
= (n∈
(n∈ ),
),
数列{an}的前n项和A =
= (n∈
(n∈ );
);
(2)∵ (n∈
(n∈ ),
),
∴数列{bn}的前n项Sn为


 .
.
考点:1、等差数列;2、拆项法求特列数列的前 项和.
项和.

练习册系列答案
相关题目
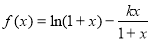 ,
,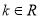 .
.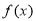 的单调区间;
的单调区间;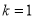 时,求
时,求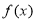 在
在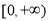 上的最小值,并证明
上的最小值,并证明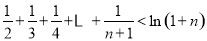 .
.
 B.
B. C.
C. D.
D.
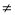 1,函数f(x)=
1,函数f(x)=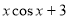 (-1
(-1 1),设函数f(x)的最大值是M,最小值是N,则( )
1),设函数f(x)的最大值是M,最小值是N,则( ) 的图象在点(1,f(1))处的切线方程是
的图象在点(1,f(1))处的切线方程是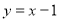 ,函数g(x)=
,函数g(x)= 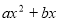 (a、b∈R,a≠0)在x=2处取得极值-2.
(a、b∈R,a≠0)在x=2处取得极值-2. (其中
(其中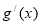 是g(x)的导函数)在区间(
是g(x)的导函数)在区间( ,
,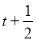 )没有单调性,求实数
)没有单调性,求实数 的取值范围;
的取值范围; 时,不等式
时,不等式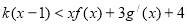 恒成立,求k的最大值.
恒成立,求k的最大值. ,则cos(
,则cos( )的值为 .
)的值为 . ,则
,则 .
. 与
与 互为共轭复数,则复数
互为共轭复数,则复数 =( ).
=( ). B.
B. C.
C. D.
D. 