题目内容
【题目】已知椭圆![]() :
:![]() (
(![]() )的离心率为
)的离心率为![]() ,且过点
,且过点![]() ,椭圆
,椭圆![]() 的右顶点为
的右顶点为![]() .
.
(Ⅰ)求椭圆的![]() 的标准方程;
的标准方程;
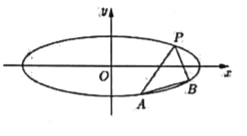
(Ⅱ)已知过点![]() 的直线交椭圆
的直线交椭圆![]() 于
于![]() ,
,![]() 两点,且线段
两点,且线段![]() 的中点为
的中点为![]() ,求直线
,求直线![]() 的斜率的取值范围.
的斜率的取值范围.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
试题(1)由椭圆的离心率为![]() ,且过点
,且过点![]() ,列方程组,求解
,列方程组,求解![]() ,
,![]() 即可;
即可;
(2)依题意,直线![]() 过点
过点![]() ,①当直线
,①当直线![]() 的斜率不为0时,可设其方程为
的斜率不为0时,可设其方程为![]() ,联立
,联立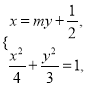 消去
消去![]() 得
得![]() ,由韦达定理、中点坐标公式,结合已知条件能求出直线
,由韦达定理、中点坐标公式,结合已知条件能求出直线![]() 的斜率的取值范围,②当直线
的斜率的取值范围,②当直线![]() 的斜率为0时,线段
的斜率为0时,线段![]() 的中点
的中点![]() 与坐标原点重合,
与坐标原点重合,![]() 的斜率为0.
的斜率为0.
试题解析:
(Ⅰ)依题意,![]() ,
,![]() ,
,![]() ,
,
解得![]() ,
,![]() ,
,![]() ,
,
故椭圆![]() 的标准方程为
的标准方程为![]() .
.
(Ⅱ)依题意,直线![]() 过点
过点![]() .①当直线
.①当直线![]() 的斜率不为0时,可设其方程为
的斜率不为0时,可设其方程为![]() ,
,
联立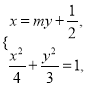 消去
消去![]() 得
得![]() ,
,
设点![]() ,
,![]() ,
,![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,
,
故![]() ,
,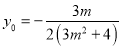 ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,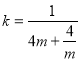 ,因为
,因为![]()
![]() ,故
,故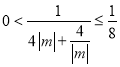 ,
,
当且仅当![]() ,即
,即![]() 时等号成立.
时等号成立.
故![]() ,故
,故![]() 且
且![]() .
.
②当直线![]() 的斜率为0时,线段
的斜率为0时,线段![]() 的中点
的中点![]() 与坐标原点重合,
与坐标原点重合,![]() 的斜率为0.
的斜率为0.
综上所述,直线![]() 的斜率的取值范围为
的斜率的取值范围为![]() .
.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目