题目内容
已知函数f(x)=sin(x+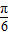 )+
)+ ,若将函数f(x)的图象向右平移
,若将函数f(x)的图象向右平移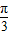 个单位后,再将得到的图象上各点横坐标伸长到原来的2倍,纵坐标不变,得到函数y=g(x)的图象
个单位后,再将得到的图象上各点横坐标伸长到原来的2倍,纵坐标不变,得到函数y=g(x)的图象(1)求函数g(x)的解析式
(2)求x为何值时,函数g(x)的值最大且最大值为多少?
(3)求g(x)单调递减区间.
【答案】分析:(1)利用函数y=Asin(ωx+φ)的图象变换即可取得函数g(x)的解析式;
(2)由 x-
x-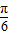 =2kπ+
=2kπ+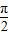 (k∈Z)即可求得函数g(x)的值最大时x的取值;
(k∈Z)即可求得函数g(x)的值最大时x的取值;
(3)由正弦函数的单调性可知,由2kπ+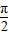 ≤
≤ x-
x-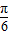 ≤2kπ+
≤2kπ+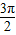 (k∈Z),即可求得g(x)单调递减区间.
(k∈Z),即可求得g(x)单调递减区间.
解答:解:(1)∵f(x)=sin(x+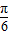 )+
)+ ,
,
∴f(x-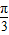 )=sin[(x-
)=sin[(x-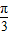 )+
)+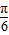 ]+
]+ =sin(x-
=sin(x-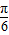 )+
)+ ;
;
再将得到的图象上各点横坐标伸长到原来的2倍,纵坐标不变,得到函数y=g(x)=sin( x-
x-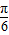 )+
)+ ;
;
∴经过题设的变化得到的函数g(x)=sin( x-
x-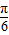 )+
)+ ;
;
(2)由 x-
x-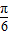 =2kπ+
=2kπ+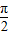 (k∈Z)得:x=4kπ+
(k∈Z)得:x=4kπ+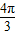 ,k∈Z
,k∈Z
∴当x=4kπ+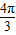 ,k∈Z时,函数取得最大值
,k∈Z时,函数取得最大值 ;
;
(3)令2kπ+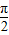 ≤
≤ x-
x-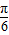 ≤2kπ+
≤2kπ+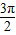 (k∈Z),
(k∈Z),
得4kπ+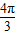 ≤x≤4kπ+
≤x≤4kπ+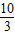 π,k∈Z
π,k∈Z
∴g(x)单调递减区间为[4kπ+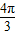 ,4kπ+
,4kπ+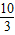 π],k∈Z.
π],k∈Z.
点评:本题考查函数y=Asin(ωx+φ)的图象变换,着重考查正弦函数的单调性与最值,属于中档题.
(2)由
 x-
x-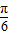 =2kπ+
=2kπ+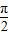 (k∈Z)即可求得函数g(x)的值最大时x的取值;
(k∈Z)即可求得函数g(x)的值最大时x的取值;(3)由正弦函数的单调性可知,由2kπ+
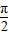 ≤
≤ x-
x-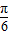 ≤2kπ+
≤2kπ+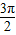 (k∈Z),即可求得g(x)单调递减区间.
(k∈Z),即可求得g(x)单调递减区间.解答:解:(1)∵f(x)=sin(x+
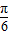 )+
)+ ,
,∴f(x-
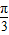 )=sin[(x-
)=sin[(x-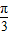 )+
)+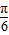 ]+
]+ =sin(x-
=sin(x-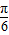 )+
)+ ;
;再将得到的图象上各点横坐标伸长到原来的2倍,纵坐标不变,得到函数y=g(x)=sin(
 x-
x-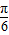 )+
)+ ;
;∴经过题设的变化得到的函数g(x)=sin(
 x-
x-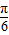 )+
)+ ;
;(2)由
 x-
x-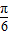 =2kπ+
=2kπ+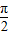 (k∈Z)得:x=4kπ+
(k∈Z)得:x=4kπ+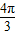 ,k∈Z
,k∈Z∴当x=4kπ+
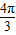 ,k∈Z时,函数取得最大值
,k∈Z时,函数取得最大值 ;
;(3)令2kπ+
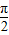 ≤
≤ x-
x-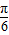 ≤2kπ+
≤2kπ+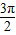 (k∈Z),
(k∈Z),得4kπ+
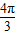 ≤x≤4kπ+
≤x≤4kπ+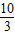 π,k∈Z
π,k∈Z∴g(x)单调递减区间为[4kπ+
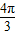 ,4kπ+
,4kπ+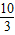 π],k∈Z.
π],k∈Z.点评:本题考查函数y=Asin(ωx+φ)的图象变换,着重考查正弦函数的单调性与最值,属于中档题.

练习册系列答案
相关题目
