题目内容
在锐角三角形ABC中,a,b,c分别是角A、B、C的对边, =(c-a,b-c)且
=(c-a,b-c)且
(1)求A的大小;
(2)记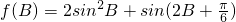 ,求f(B)的取值范围.
,求f(B)的取值范围.
解:(1)由题意知 ⊥
⊥ ,所以
,所以 •
• =(a+c)(c-a)+b(b-c)=0,
=(a+c)(c-a)+b(b-c)=0,
即b2+c2-a2=bc.
在△ABC,由余弦定理知:
 =
= .
.
又∵A∈(0,π),
∴ .
.
(2)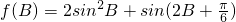
= .
.
又△ABC为锐角三角形,
所以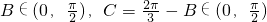 ,
,
即 ,
,
∴ ,
,
所以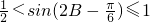 ,
,
故f(B)的取值范围是( ,2].
,2].
分析:(1)根据两个向量垂直,得到两个向量的数量积等于0,得到关于三角形的边长之间的关系,符合余弦定理,根据角A的范围和余弦值,做出角A的大小.
(2)首先对所给的三角函数式进行整理,利用二倍角公式和两角和与差的正弦公式,得到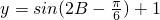 ,根据角B的范围,确定所用的角的范围,根据正弦函数的值域得到结果.
,根据角B的范围,确定所用的角的范围,根据正弦函数的值域得到结果.
点评:本题考查及三角形的问题,考查三角函数的恒等变形化简求值,角的范围的讨论和三角函数在某一个区间上的最值,本题解题的关键是对于函数式的整理,本题的易错点是对于角的范围的分析,注意三角形中的隐含条件,合理地进行等价转化.
 ⊥
⊥ ,所以
,所以 •
• =(a+c)(c-a)+b(b-c)=0,
=(a+c)(c-a)+b(b-c)=0,即b2+c2-a2=bc.
在△ABC,由余弦定理知:
 =
= .
.又∵A∈(0,π),
∴
 .
.(2)
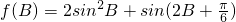
=
 .
.又△ABC为锐角三角形,
所以
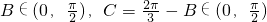 ,
,即
 ,
,∴
 ,
,所以
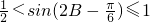 ,
,故f(B)的取值范围是(
 ,2].
,2].分析:(1)根据两个向量垂直,得到两个向量的数量积等于0,得到关于三角形的边长之间的关系,符合余弦定理,根据角A的范围和余弦值,做出角A的大小.
(2)首先对所给的三角函数式进行整理,利用二倍角公式和两角和与差的正弦公式,得到
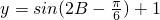 ,根据角B的范围,确定所用的角的范围,根据正弦函数的值域得到结果.
,根据角B的范围,确定所用的角的范围,根据正弦函数的值域得到结果.点评:本题考查及三角形的问题,考查三角函数的恒等变形化简求值,角的范围的讨论和三角函数在某一个区间上的最值,本题解题的关键是对于函数式的整理,本题的易错点是对于角的范围的分析,注意三角形中的隐含条件,合理地进行等价转化.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目