题目内容
如图，ABCD是矩形，VA⊥平面ABCD，AK上VC于K，KE⊥VC交VB于E，KH⊥VC交VD于H．求证：K、H、A、E四点共面且共圆．
答案：略
解析：
解析：
|
∵ AK⊥VC，KE⊥VC，AK∩KE＝K，∴VC⊥平面AKE．同理可证VC⊥平面EHK．但平面EHK与平面AEK有公共点K，∴两平面重合．∴A、E、K、H四点共面．又∵VA⊥平面ABCD，ABCD为矩形，∴VA⊥BC，AB⊥BC．∵BC⊥平面VAB．∴AE⊥BC，且AE⊥VC．BC∩VC＝C，∵AE⊥平面VBC．∴AE⊥EK．同理可证AH⊥HK．∴∠AHK＋∠AEK＝180°．∴A、E、K、H四点共圆． |
练习册系列答案
相关题目
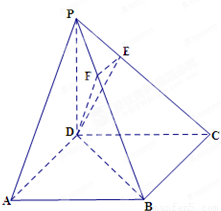
如图，ABCD是矩形，过点D作PD⊥平面ABCD，连接PA、PB、PC，E是PC上的一点，且DE⊥PC，过E作EF⊥PB于F．
