题目内容
设{an}是集合{2t+2s|0≤s<t,且s,t∈Z}中所有的数从小到大排列成的数列,即a1=3,a2=5,a3=6,a4=9,a5=10,a6=12,….
(1)将数列{an}各项按照上小下大,左小右大的原则写成如下的三角形数表:
注:本题考查归纳猜想的能力.
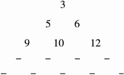
①写出这个三角形数表的第四行,第五行各数;
②求a100.
(2)设{bn}是集合{2t+2s+2r|0≤r<s<t,且r,s,t∈Z}中所有的数从小到大排列成的数列,已知bk=1160,求k.
解析:
|
(1)①解:第四行17 18 20 24 第五行 33 34 36 40 48 ②解法一:设a100=2t0+2s0.只需确定正整数t0,s0. 数列{an}中小于2t0的项构成的子集为{2t+2s|0≤s<t<t0}. 其元素个数为C2t0= 依题意 满足上式的最大整数t0为14,所以取t0=14. 因为100-C214=s0+1,由此解得s0=8. 所以a100=214+28=16640. 解法二:n为an的下标,三角形数表第一行第一个元素下标为1, 第二行第一个元素下标为 第三行第一个元素下标为 …… 第t行第一个元素下标为 据此判断a100所在的行,因为 (2)解:bk=1160=210+2++23, 令M={c∈B|c<1160}(其中B={2t+2s+2r|0≤r<s<t}), 因M={c∈B|c<210}∪{c∈B|210<c<210+27}∪{c∈B|210+27<c<210+27+23}. 现在求M的元素个数:{c∈B|c<210}={2t+2s+2r|0≤r<s<t<10},其元素个数为C310; {c∈B|210<c<210+27}={210+2s+2r|0≤r<s<7}. 其元素个数为C27; {c∈B|210+27<c<210+27+23}={210+27+2r|0≤r<3}; 其元素个数为C13; ∴k= |

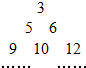 设an是集合2s+2t|0≤s<t,s,t∈Z中所有的数从小到大排列成的数列,即a1=3,a2=5,a3=6,a4=9,a5=10,a6=12,…,将数列an各项按照上小下大、左小右大的原则写成如下的三角形数表:
设an是集合2s+2t|0≤s<t,s,t∈Z中所有的数从小到大排列成的数列,即a1=3,a2=5,a3=6,a4=9,a5=10,a6=12,…,将数列an各项按照上小下大、左小右大的原则写成如下的三角形数表: 设{an}是集合{2t+2s|0≤s<t,且s,t∈z}中所有的数从小到大排列成的数列,即a1=3,a2=5,a3=6,a4=9,a5=10,a6=12,…将数列{an}各项按照上小下大,左小右大的原则写成如图的三角形数表:
设{an}是集合{2t+2s|0≤s<t,且s,t∈z}中所有的数从小到大排列成的数列,即a1=3,a2=5,a3=6,a4=9,a5=10,a6=12,…将数列{an}各项按照上小下大,左小右大的原则写成如图的三角形数表: