题目内容
已知函数f(x)=(sinx+cosx)2-2sin2x
(1)求f(x)的最小正周期:
(2)函数y=g(x)的图象是由y=f(x)的图象向左平移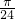 个单位长度,再将图象上点的横坐标伸长为原来的2倍得到的,若角A为三角形的最小内角,求g(A)的取值范围.
个单位长度,再将图象上点的横坐标伸长为原来的2倍得到的,若角A为三角形的最小内角,求g(A)的取值范围.
解:(1)∵f(x)=(sinx+cosx)2-2sin2x=1+sin2x-2× =1+sin2x-1-cos2x
=1+sin2x-1-cos2x
=sin2x-cos2x= sin(2x-
sin(2x- ),
),
故函数的最小正周期为 =π.
=π.
(2)把y=f(x)的图象向左平移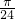 个单位长度所得图象对应的函数解析式为y=
个单位长度所得图象对应的函数解析式为y= sin[2(x-
sin[2(x-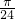 )-
)- ]
]
= sin(2x-
sin(2x- ),
),
再将图象上点的横坐标伸长为原来的2倍得到函数y= sin(x-
sin(x- ) 的图象,
) 的图象,
故由题意可得g(x)= sin(x-
sin(x- ),故g(A)=
),故g(A)= sin(A-
sin(A- ).
).
若角A为三角形的最小内角,则有0<A≤ ,∴-
,∴- <A-
<A- ≤0,-
≤0,- <sin(A-
<sin(A- )≤0,
)≤0,
故- <
< sin(A-
sin(A- )≤0,
)≤0,
故g(A)的取值范围为(- ,0].
,0].
分析:(1)利用三角函数的恒等变换化简函数f(x)的解析式为 sin(2x-
sin(2x- ),由此求得函数的最小正周期.
),由此求得函数的最小正周期.
(2)把y=f(x)的图象经过两次变换后得到所得图象对应的函数解析式为g(x)= sin(x-
sin(x- ),故g(A)=
),故g(A)= sin(A-
sin(A- ),再根据0<A≤
),再根据0<A≤ ,求出g(A)的取值范围.
,求出g(A)的取值范围.
点评:本题主要考查三角函数的恒等变换及化简求值,三角函数的周期性与求法,函数y=Asin(ωx+∅)的图象变换,属于中档题.
 =1+sin2x-1-cos2x
=1+sin2x-1-cos2x=sin2x-cos2x=
 sin(2x-
sin(2x- ),
),故函数的最小正周期为
 =π.
=π.(2)把y=f(x)的图象向左平移
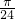 个单位长度所得图象对应的函数解析式为y=
个单位长度所得图象对应的函数解析式为y= sin[2(x-
sin[2(x-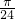 )-
)- ]
]=
 sin(2x-
sin(2x- ),
),再将图象上点的横坐标伸长为原来的2倍得到函数y=
 sin(x-
sin(x- ) 的图象,
) 的图象,故由题意可得g(x)=
 sin(x-
sin(x- ),故g(A)=
),故g(A)= sin(A-
sin(A- ).
).若角A为三角形的最小内角,则有0<A≤
 ,∴-
,∴- <A-
<A- ≤0,-
≤0,- <sin(A-
<sin(A- )≤0,
)≤0,故-
 <
< sin(A-
sin(A- )≤0,
)≤0,故g(A)的取值范围为(-
 ,0].
,0].分析:(1)利用三角函数的恒等变换化简函数f(x)的解析式为
 sin(2x-
sin(2x- ),由此求得函数的最小正周期.
),由此求得函数的最小正周期.(2)把y=f(x)的图象经过两次变换后得到所得图象对应的函数解析式为g(x)=
 sin(x-
sin(x- ),故g(A)=
),故g(A)= sin(A-
sin(A- ),再根据0<A≤
),再根据0<A≤ ,求出g(A)的取值范围.
,求出g(A)的取值范围.点评:本题主要考查三角函数的恒等变换及化简求值,三角函数的周期性与求法,函数y=Asin(ωx+∅)的图象变换,属于中档题.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|