Question

已知函数f(x)=2^x-2^-x,数列{a_n}满足f(log₂a_n)=-2n.

(1)求数列{a_n}的通项公式;

(2)讨论数列{a_n}的单调性,并证明你的结论.

   

Answer 1

思路分析:本题主要考查利用函数的观点解决数列问题.(1)由于f(log₂a_n)=-2n,利用f(x)=2^x-2^-x便可得到关于a_n的方程,解得a_n即可.(2)讨论数列的单调性,即比较每相邻两项a_n与a_n+1的大小.若a_n+1＞a_n,则｛a_n｝为单调递增数列;若a_n+1＜a_n,则{a_n}为单调递减数列.

    解:(1)∵f(x)=2^x-2^-x,f(log₂a_n)=-2n,

∴有=-2n,即a_n-=-2n.

∴a_n²+2na_n-1=0,解得a_n=-n±.

∵a_n＞0,∴a_n=-n.

(2)作商比较.

∵=

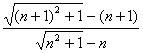
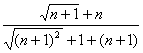=＜1,

    又a_n＞0,

∴a_n+1＜a_n,故数列{a_n}是递减数列.