题目内容
已知函数F(x)=(1)判断函数F(x)在区间(0,1)上的单调性,并证明你的结论;
(2)求函数F(x)的最小值;
(3)当0<x1<x2<1时,证明F(![]() )<
)<![]() .
.
(1)解:f(x)在区间(0,1)上是减函数.证明如下:?
当0<x<1时,f(x)=![]() +x-1.?
+x-1.?
∵f′(x)=(![]() +x-1)′=1-
+x-1)′=1-![]() =
=![]() <0,?
<0,?
∴f(x)在区间(0,1)上是减函数. ?
(2)解:∵f(x)在(0,1]上是减函数,∴当x∈(0,1]时,f(x)≥f(1)=1.?
又∵x>1时,lnx>0,x-1>0,?
∴f(x)=Elnx-(x-1)=x-(x-1)=1.?
∴x∈(0,+∞)时,f(x)≥1,?
即函数f(x)的最小值为1,当且仅当x≥1时取得. ?
(3)证明:∵当0<x<1时,f(x)=![]() +x-1,?
+x-1,?
∴当0<x1<x2<1时,0<![]() <1.?
<1.?
∴f(![]() )=
)=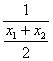 +
+![]() -1=
-1=![]() +
+![]() -1,?
-1,?
![]() =
=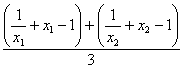 =
=![]() -1+
-1+![]() <
<![]() -1+
-1+
![]() =
=![]() +
+![]() -1,?
-1,?
∴![]() <f(
<f(![]() ).
).

练习册系列答案
相关题目
 已知函数f(x)=
已知函数f(x)=
|
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、[
|