题目内容
已知f(x)是定义在R上的偶函数,若g(x)是奇函数,且g(x)=f(x-1),g(2)=2 008,则f(2 007)的值等于______________.
2 008 ∵g(x)为奇函数,f(x)为偶函数,
∴-g(x)=g(-x)=f(-x-1)=f[-(x+1)]=f(x+1).
∴f(x+1)=-g(x).∴f(x+2)=f[(x+1)+1]=-g(x+1)=-f(x).
∴f(x+4)=f(x),∴f(x)的周期为T=4.
∴f(2 007)=f(2 004+3)=f(3)=f(-1)=f(1)=g(2)=2 008.

练习册系列答案
相关题目
 ) =
f(x)-f(y)
) =
f(x)-f(y) 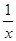 ) <2
) <2  ∪
∪ 上的奇函数,当
上的奇函数,当 时,f (x)的图象如图所示,那么f (x)的值域是
时,f (x)的图象如图所示,那么f (x)的值域是
