题目内容
已知函数 .
.(1)当m=-1时,求函数f(x)的最大值;
(2)当m=1时,设点A、B是函数y=f(x)(x∈[0,1])的图象上任意不同的两点,求证:直线AB的斜率kAB<2.
【答案】分析:(1)对函数求导,根据定义域,结合函数的导函数确定函数的单调性,从而可确定函数的最值;
(I2)当m=1时,利用斜率的定义,构造新函数得到函数在[0,1]上递减,即可得到结论.
解答:(1)解:m=-1时,
求导函数,可得:f′(x)= .
.
令f′(x)>0,可得- <x<0,令f′(x)<0,可得x>0,
<x<0,令f′(x)<0,可得x>0,
∴x=0时,函数取得最大值0;
(2)证明:当m=1时,
设点A(x1,f(x1)),B(x2,f(x2)),x1,x2∈[0,1],x1<x2
∴kAB<2,等价于 ,∴f(x2)-2x2<f(x1)-2x1
,∴f(x2)-2x2<f(x1)-2x1
令h(x)=f(x)-2x= ,由(1)知它在[0,1]上递减,
,由(1)知它在[0,1]上递减,
∵x1,x2∈[0,1],x1<x2
∴h(x1)>h(x2)
即f(x2)-2x2<f(x1)-2x1
综上所述,当m=1时,直线AB的斜率kAB<2
点评:本题考查函数的单调性与导数的关系,考查根据需要构造新函数,考查解决问题的能力和分析问题的能力,是一个中档题.
(I2)当m=1时,利用斜率的定义,构造新函数得到函数在[0,1]上递减,即可得到结论.
解答:(1)解:m=-1时,

求导函数,可得:f′(x)=
 .
.令f′(x)>0,可得-
 <x<0,令f′(x)<0,可得x>0,
<x<0,令f′(x)<0,可得x>0,∴x=0时,函数取得最大值0;
(2)证明:当m=1时,

设点A(x1,f(x1)),B(x2,f(x2)),x1,x2∈[0,1],x1<x2
∴kAB<2,等价于
 ,∴f(x2)-2x2<f(x1)-2x1
,∴f(x2)-2x2<f(x1)-2x1令h(x)=f(x)-2x=
 ,由(1)知它在[0,1]上递减,
,由(1)知它在[0,1]上递减,∵x1,x2∈[0,1],x1<x2
∴h(x1)>h(x2)
即f(x2)-2x2<f(x1)-2x1
综上所述,当m=1时,直线AB的斜率kAB<2
点评:本题考查函数的单调性与导数的关系,考查根据需要构造新函数,考查解决问题的能力和分析问题的能力,是一个中档题.

练习册系列答案
相关题目
 .
. 上的取值范围;
上的取值范围; ,求m的值.
,求m的值. .
. 上的取值范围;
上的取值范围; ,求m的值.
,求m的值.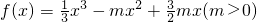 .
.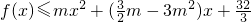 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.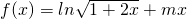 .
. .
.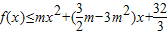 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.