题目内容
14、若f(x)=|x-t|+|5-x|的最小值为3,则实数t的值是
2或8
.分析:首先分析题目已知不等式f(x)=|x-t|+|5-x|最小值为3,求实数t的值.考虑到根据绝对值不等式的性质,绝对值之和大于等于和的绝对值.即可求出f(x)≥|5-t|,即令|5-t|等于最小值即可解得答案.
解答:解:因为根据绝对值不等式的性质可以得到
f(x)=|x-t|+|5-x|≥|(x-t)+(5-x)|=|5-t|
又已知f(x)=|x-t|+|5-x|最小值为3,
故有|5-t|=3,即可解出t=2或8.
故答案为:2或8.
f(x)=|x-t|+|5-x|≥|(x-t)+(5-x)|=|5-t|
又已知f(x)=|x-t|+|5-x|最小值为3,
故有|5-t|=3,即可解出t=2或8.
故答案为:2或8.
点评:此题主要考查绝对值不等式的性质“绝对值之和大于和的绝对值”的应用,避免了分类讨论去绝对值的繁琐,有一定的技巧性,属于中档题目.

练习册系列答案
相关题目
设函数f(x)的定义域为A,若存在非零实数t,使得对于任意x∈C(C⊆A),有x+t∈A,且f(x+t)≤f(x),则称f(x)为C上的t低调函数.如果定义域为[0,+∞)的函数f(x)=-|x-m2|+m2,且 f(x)为[0,+∞)上的10低调函数,那么实数m的取值范围是( )
| A、[-5,5] | ||||||||
B、[-
| ||||||||
C、[-
| ||||||||
D、[-
|
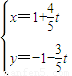 (t为参数)被曲线
(t为参数)被曲线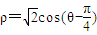 所截的弦长为 .
所截的弦长为 .