题目内容
已知菱形ABCD的边长为2,∠DAB=60°,E、F分别为CD,BC的中点,则 =________.
=________.

分析:由题意可得,
 与
与 的夹角等于60°,且
的夹角等于60°,且 =(
=( )•(
)•( ),利用两个向量的数量积的定义,运算求得结果.
),利用两个向量的数量积的定义,运算求得结果.解答:由题意可得,
 与
与 的夹角等于60°,
的夹角等于60°, =(
=( )•(
)•( )=
)= -
-
 +
+
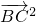 -
-

=

 =
= =
= ,
,故答案为
 .
.点评:本题主要考查两个向量的加减法的法则,以及其几何意义,两个向量的数量积的定义,属于中档题.

练习册系列答案
相关题目
 如图,已知菱形ABCD的边长为6,∠BAD=60°,AC∩BD=O.将菱形ABCD沿对角线AC折起,使
如图,已知菱形ABCD的边长为6,∠BAD=60°,AC∩BD=O.将菱形ABCD沿对角线AC折起,使

 如图,已知菱形ABCD的边长为2,∠BAD=60°,S为平面ABCD外一点,△SAD为正三角形,
如图,已知菱形ABCD的边长为2,∠BAD=60°,S为平面ABCD外一点,△SAD为正三角形,