题目内容
已知函数f(x)=sinxcosx+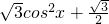 (x∈R)
(x∈R)
(1)求函数f(x)的最小正周期;
(2)求函数f(x)的单调减区间;
(3)求函数f(x)的对称轴方程,对称中心的坐标.
解:由题意f(x)=sinxcosx+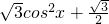
= sin2x+
sin2x+ cos2x
cos2x
=sin(2x- )
)
(1)T= =π
=π
(2)令2kπ+ ≤2x-
≤2x- ≤2kπ+
≤2kπ+ ,k∈z
,k∈z
解得kπ+ ≤x≤kπ+
≤x≤kπ+ ,k∈z
,k∈z
函数f(x)的单调减区间是[kπ+ ,kπ+
,kπ+ ]k∈z
]k∈z
(3)令2x- =kπ+
=kπ+ ,解得x=kπ+
,解得x=kπ+ ,k∈z即为函数的对称轴方程;
,k∈z即为函数的对称轴方程;
可令2x- =kπ,k∈z,解得x=
=kπ,k∈z,解得x=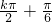 ,对称中心的坐标是(
,对称中心的坐标是(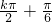 ,0),k∈z
,0),k∈z
分析:先用恒等变换公式对函数f(x)化简整理,易得f(x)=sinxcosx+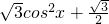 =sin(2x-
=sin(2x- )
)
(1)求函数f(x)的最小正周期,用周期公式求解即可;
(2)求函数f(x)的单调减区间,利用正弦函数的性质,令2kπ+ ≤2x-
≤2x- ≤2kπ+
≤2kπ+ ,k∈z即可解出;
,k∈z即可解出;
(3)求函数f(x)的对称轴方程,可令2x- =kπ+
=kπ+ ,k∈z求对称中心坐标可令2x-
,k∈z求对称中心坐标可令2x- =kπ,k∈z
=kπ,k∈z
点评:本题考查三角函数恒等变换应用、三角函数的周期性的求法,函数的单调递减区间等,解题关键是掌握住三角恒等变换公式,以及三角函数的性质.
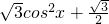
=
 sin2x+
sin2x+ cos2x
cos2x=sin(2x-
 )
)(1)T=
 =π
=π(2)令2kπ+
 ≤2x-
≤2x- ≤2kπ+
≤2kπ+ ,k∈z
,k∈z解得kπ+
 ≤x≤kπ+
≤x≤kπ+ ,k∈z
,k∈z函数f(x)的单调减区间是[kπ+
 ,kπ+
,kπ+ ]k∈z
]k∈z(3)令2x-
 =kπ+
=kπ+ ,解得x=kπ+
,解得x=kπ+ ,k∈z即为函数的对称轴方程;
,k∈z即为函数的对称轴方程;可令2x-
 =kπ,k∈z,解得x=
=kπ,k∈z,解得x=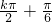 ,对称中心的坐标是(
,对称中心的坐标是(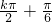 ,0),k∈z
,0),k∈z分析:先用恒等变换公式对函数f(x)化简整理,易得f(x)=sinxcosx+
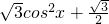 =sin(2x-
=sin(2x- )
)(1)求函数f(x)的最小正周期,用周期公式求解即可;
(2)求函数f(x)的单调减区间,利用正弦函数的性质,令2kπ+
 ≤2x-
≤2x- ≤2kπ+
≤2kπ+ ,k∈z即可解出;
,k∈z即可解出;(3)求函数f(x)的对称轴方程,可令2x-
 =kπ+
=kπ+ ,k∈z求对称中心坐标可令2x-
,k∈z求对称中心坐标可令2x- =kπ,k∈z
=kπ,k∈z点评:本题考查三角函数恒等变换应用、三角函数的周期性的求法,函数的单调递减区间等,解题关键是掌握住三角恒等变换公式,以及三角函数的性质.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案
相关题目
