题目内容
已知函数f(x)=alnx-bx2图象上一点P(2,f(2))处的切线方程为y=-3x+2ln2+2。
(1)求a,b的值;
(2)若方程f(x)+m=0在 内有两个不等实根,求m的取值范围(其中e为自然对数的底);
内有两个不等实根,求m的取值范围(其中e为自然对数的底);
(3)令g(x)=f(x)-nx,如果g(x)图象与x轴交于A(x1,0),B(x2,0)(x1<x2),AB中点为C(x0,0),求证:g′(x0)≠0。
(1)求a,b的值;
(2)若方程f(x)+m=0在
 内有两个不等实根,求m的取值范围(其中e为自然对数的底);
内有两个不等实根,求m的取值范围(其中e为自然对数的底);(3)令g(x)=f(x)-nx,如果g(x)图象与x轴交于A(x1,0),B(x2,0)(x1<x2),AB中点为C(x0,0),求证:g′(x0)≠0。
解:(1)f′(x)=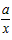 -2bx,f′(2)=
-2bx,f′(2)=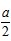 -4b,f(2)=aln2-4b,
-4b,f(2)=aln2-4b,
∴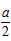 -4b=-3,且aln2-4b=-6+2ln2+2,
-4b=-3,且aln2-4b=-6+2ln2+2,
解得a=2,b=1;
(2)f(x)=2lnx-x2,令h(x)=f(x)+m=2lnx-x2+m,
则h′(x)=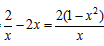 ,令h′(x)=0,得x=1(x=-1舍去),
,令h′(x)=0,得x=1(x=-1舍去),
在[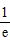 ,e]内,当x∈[
,e]内,当x∈[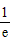 ,1)时,h′(x)>0,所以h(x)是增函数;
,1)时,h′(x)>0,所以h(x)是增函数;
当x∈(1,e]时,h′(x)<0,所以h(x)是减函数,
则方程h(x)=0在[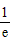 ,e]内有两个不等实根的充要条件是
,e]内有两个不等实根的充要条件是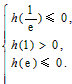
即1<m≤e2-2;
(3)g(x)=2lnx-x2-nx,g′(x)= -2x-n,
-2x-n,
假设结论成立,则有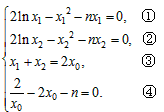
①-②,得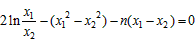
∴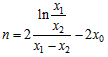 ,
,
由④得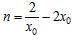 ,
,
∴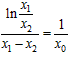 ,即
,即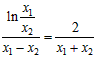 ,
,
即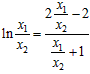 ,⑤,
,⑤,
令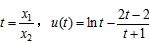 (0<t<1),
(0<t<1),
则u′(t)=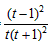 >0,所以u(t)在0<t<1上是增函数,
>0,所以u(t)在0<t<1上是增函数,
u(t)<u(1)=0,
所以⑤式不成立,与假设矛盾,
所以g′(x0)≠0。

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目