Question

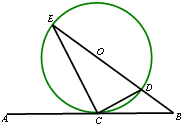
（2012•江苏二模）选修4-1：几何证明选讲
如图，直线AB经过圆O上的点C，并且OA=OB，CA=CB，圆O交直线OB于E，D，连接EC，CD，若tan∠CED=

1

2

，圆O的半径为3，求OA的长．

Answer 1

分析：利用圆的直径、切线的性质及弦切角定理、切割线定理、三角形相似的判定与性质即可得出．

解答：解：如图，连OC，∵OA=OB，CA=CB，∴OC⊥AB．
∵OC是圆的半径，∴AB是圆的切线．
∵ED是圆O的直径，∴∠ECD=90°．
在Rt△ECD中，tan∠ECD=

CD

CE

=

1

2

．
由弦切角定理可得∠BCD=∠BEC，又∠B公用，
∴△BCD∽△BEC，∴

BD

BC

=

CD

EC

=

1

2

，BC²=BD（BD+6）．
化为（2BD）²=BD（BD+6），解得BD=2，
∴OA=OB=OD+DB=3+2=5．

点评：熟练掌握圆的直径、切线的性质及弦切角定理、切割线定理、三角形相似的判定与性质是解题的关键．