Question

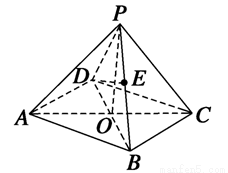
（本小题满分12分）如图所示，在四棱锥P—ABCD中，底面是边长为2的菱形，∠DAB=60°，对角线AC与BD交于点O，PO⊥平面ABCD，PB与平面ABCD所成角为60°.

（1）求四棱锥的体积；

（2）若E是PB的中点，求异面直线DE与PA所成角的余弦值.

 

Answer 1

【答案】

（1）V_P—ABCD=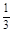×2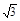×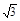=2.  （2）异面直线DE与PA所成角的余弦值为.

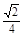【解析】本试题主要是考查了四棱锥的体积和异面直线的所成的角的求解问题。

（1）底面是菱形，根据锥体的体积公式得到高度和底面积，得到求解。

（2））取AB的中点F，连接EF，DF，

∵E为PB中点，∴EF∥PA，

∴∠DEF为异面直线DE与PA所成角（或其补角）然后借助于解三角形得到结论。

解  （1）在四棱锥P—ABCD中，

∵PO⊥平面ABCD，

∴∠PBO是PB与平面ABCD所成的角，

即∠PBO=60°，                                          ……1分

在Rt△POB中，

∵BO=AB·sin30°=1，

又PO⊥OB，∴PO=BO·tan60°=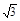,       ………2分

∵底面菱形的面积S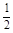=2××2×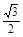2×=2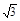.………3分

∴四棱锥P—ABCD的体积

V_P—ABCD=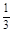×2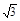×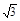=2.                               5分

（2）取AB的中点F，连接EF，DF，

∵E为PB中点，∴EF∥PA，

∴∠DEF为异面直线DE与PA所成角（或其补角）. ………7分    

在Rt△AOB中，

AO=AB·cos30°=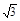=OP，

∴在Rt△POA中，PA=6，∴EF=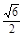.………9分

在正三角形ABD和正三角形PDB中，DF=DE=，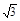

由余弦定理得

∴cos∠DEF=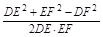     

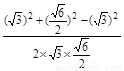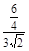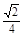===.………11分

所以异面直线DE与PA所成角的余弦值为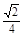.                    12分