题目内容
19.设抛物线y2=2px(p>0)的焦点为F，经过点F的直线交抛物线于A、B两点.点C在抛物线的准线上，
且BC∥x轴.证明直线AC经过原点O.
19.本小题考查抛物线的概念和性质，直线的方程和性质，运算能力和逻辑推理能力.
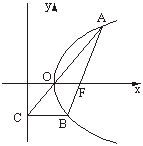
证明一：因为抛物线y2=2px(p>0)的焦点为F(
)，所以经过点F的直线AB的方程可设为x=my+
；
代入抛物线方程得y2－2pmy－p2=0,
若记A(x1,y1),B(x2,y2),则y1,y2是该方程的两个根，所以y1y2=－p2.
因为BC∥x轴，且点C在准线x=－
上，所以点C的坐标为(－
，y2),故直线CO的斜率为
k=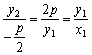
.
即k也是直线OA的斜率，所以直线AC经过原点O.
证明二：如图，记x轴与抛物线准线l的交点为E，过A作AD⊥l，D是垂足.
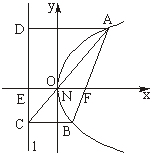
则AD∥EF∥BC.
连结AC，与EF相交于点N，则
，
，
根据抛物线的几何性质，|AF|=|AD|,|BF|=|BC|，
所以 |EN|=
=
=|NF|，
即点N是EF的中点，与抛物线的顶点O重合，所以直线AC经过原点O.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
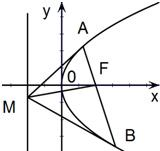设抛物线y2=2px（p＞0）的焦点为F，经过点F的直线交抛物线于A，B两点，且A，B两点坐标分别为（x1，y1）、（x2，y2），y1＞0，y2＜0，M是抛物线的准线上的一点，O是坐标原点．若直线MA，MF，MB的斜率分别记为：KMA=a，KMF=b，KMB=c，（如图）