Question

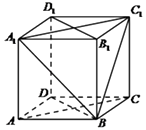
【题目】如图，三棱柱中， 平面， ， 是上的动点， .

（Ⅰ）若点是中点，证明：平面平面；

（Ⅱ）判断点到平面的距离是否为定值？若是，求出定值；若不是，请说明理由.

Answer 1

【答案】（1）见解析（2）

【解析】试题解析：按照判定定理证明面面垂直只需在一个平面内寻找一条直线与另一个平面垂直，观察图形看到就是最佳“人”选；第二步求点到平面的距离，由于有现成的垂面，可以直接向交线引垂线，直接得出线面垂直，利用三角形等面积法求出距离.

试题解析：（Ⅰ）证明： ， 是中点， .

平面， 平面， .

平面， 平面，且

平面.

平面， 平面平面.

（Ⅱ）,平面， 平面，

平面.

点到平面的距离是定值.

令点平分，作的中点，连结， ， ，过作，

垂足为，显然、、、共面.

平面， ， 平面.

平面， .又， 平面， 平面， 平面，即为所求.

， ， .

..

， .

点到平面的距离.