题目内容
函数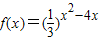
的单调递增区间为 ．
【答案】分析：令t=x2-4x，则y=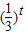
，结合二次函数的图象和性质，指数函数的图象和性质，及复合函数单调性“同增异减”的原则，可得答案．
解答：解：令t=x2-4x，则y=
∵0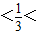
1
故y=
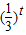为减函数
又∵t=x2-4x的单调递减区间为（-∞，2]
根据复合函数单调性“同增异减”的原则可得
函数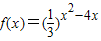
的单调递增区间为：（-∞，2]
故答案为：（-∞，2]
点评：本题考查的知识点是函数单调性的性质，熟练掌握基本初等函数的单调性及复合函数单调性“同增异减”的原则是解答的关键．
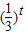，结合二次函数的图象和性质，指数函数的图象和性质，及复合函数单调性“同增异减”的原则，可得答案．解答：解：令t=x2-4x，则y=
∵0
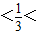1故y=
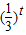为减函数又∵t=x2-4x的单调递减区间为（-∞，2]
根据复合函数单调性“同增异减”的原则可得
函数
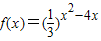的单调递增区间为：（-∞，2]故答案为：（-∞，2]
点评：本题考查的知识点是函数单调性的性质，熟练掌握基本初等函数的单调性及复合函数单调性“同增异减”的原则是解答的关键．
练习册系列答案
相关题目
的单调递增区间为________________
的单调递增区间为
。