题目内容
在下列命题中：①若两个非零向量
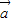和
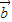共线则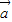 
，
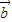所在的直线平行；②若
，
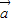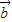所在的直线是异面直线，则
，
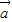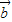一定不共面；③若
，
，
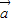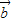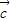三向量两两共面，则
，
，
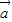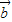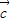三向量一定也共面；④若
，
，
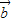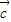是三个非零向量，则空间任意一个向量p总可以唯一表示为
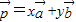+z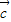
（x，y，z∈R）．其中正确命题的个数为（ ）
A．0
B．1
C．2
D．3
【答案】分析：利用两向量平行⇒两线平行或重合；任两向量通过平移都可以到一个平面上；通过举反例对各命题进行判断
解答：解：对于①，若两个非零向量
和
共线则 
，
所在的直线平行或重合，故①错
对于②，由于向量具有平移的性质，故任意的两个向量都是共面向量，故②错
对于③，例如长方体的任三条侧棱对应的向量共面，但这三条侧棱不共面，故③错
对于④，根据空间向量的基本定理及其意义，必须是三个非零向量不共面，故④错
故选A
点评：本题考查空间向量的基本定理及其意义、共线向量的几何意义；向量的平移性质；共面向量的定义．
解答：解：对于①，若两个非零向量
和共线则 ，所在的直线平行或重合，故①错对于②，由于向量具有平移的性质，故任意的两个向量都是共面向量，故②错
对于③，例如长方体的任三条侧棱对应的向量共面，但这三条侧棱不共面，故③错
对于④，根据空间向量的基本定理及其意义，必须是三个非零向量不共面，故④错
故选A
点评：本题考查空间向量的基本定理及其意义、共线向量的几何意义；向量的平移性质；共面向量的定义．
练习册系列答案
名校课堂系列答案
相关题目
）图象的一个对称中心为点（
，0）；③若函数f（x）在R上满足f（x+1）=
，则f（x）是周期为2的函数；④在△ABC中，若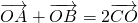
，则S△ABC=S△BOC其中正确命题的序号为________．
）图象的一个对称中心为点（
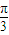，0）；③若函数f（x）在R上满足f（x+1）=
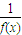，则f（x）是周期为2的函数；④在△ABC中，若
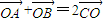，则S△ABC=S△BOC其中正确命题的序号为 ．
①已知两条不同直线
，两个不同平面
；
②函数
图象的一个对称中心为点
；
在R上满足
，则
，则
;