题目内容
在圆 内任取一点,则该点恰好在区域
内任取一点,则该点恰好在区域 内的概率为( )
内的概率为( )
A. | B. | C. | D. |
C
解析试题分析:作出不等式组 表示的平面区域,得到如下图的△ABC及其内部,其中A(1,2),B(3,3),C(3,1),∵△ABC位于圆(x-2)2+(y-2)2=4内的部分,∴在圆
表示的平面区域,得到如下图的△ABC及其内部,其中A(1,2),B(3,3),C(3,1),∵△ABC位于圆(x-2)2+(y-2)2=4内的部分,∴在圆 内任取一点,则该点恰好在区域
内任取一点,则该点恰好在区域 内的概率为
内的概率为 故答案为:
故答案为: .
.
考点:着重考查了二元一次不等式组表示的平面区域和几何概型等知识,考查学生的基本运算能力.

练习册系列答案
相关题目
若实数x,y满足不等式组 , 则x+y的最小值是( )
, 则x+y的最小值是( )
A. | B.3 | C.4 | D.6 |
已知 满足约束条件
满足约束条件 若的最小值为4,则
若的最小值为4,则 ,则
,则 ( )
( )
| A.1 | B.2 | C.3 | D.4 |
若实数 满足不等式组
满足不等式组 为常数),且
为常数),且 的最大值为12,则实数
的最大值为12,则实数 ( )
( )
A. | B. | C. | D. |
设z=x+y,其中x、y满足 ,若z的最大值为6,则z的最小值为 ( )
,若z的最大值为6,则z的最小值为 ( )
| A.-3 | B.3 | C.2 | D.-2 |
已知平面区域如右图所示, 在平面区域内取得最大值的最优解有无数多个,则
在平面区域内取得最大值的最优解有无数多个,则 的值为( )
的值为( )
A. | B. | C. | D.不存在 |
在平面直角坐标系中,若不等式组 (
(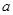 为常数)所表示平面区域的面积等于2,
为常数)所表示平面区域的面积等于2,
则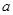 的值为( )
的值为( )
| A.-5 | B.1 | C.2 | D.3 |
实数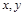 满足条件
满足条件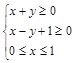 ,则
,则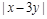 的最大值为( )
的最大值为( )
| A.6 | B.5 | C.4 | D.3 |
若变量 满足
满足 则
则 的最大值是( )
的最大值是( )
| A.90 | B.80 |
| C.50 | D.40 |