题目内容
已知函数f(x)=ax-lnx(a∈R),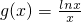 ,其中x∈(0,e]
,其中x∈(0,e]
(1)若a=1,求f(x)的极小值;
(2)在(1)条件下证明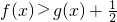 ;
;
(3)是否存在实数a>0,使f(x)的最小值为3,如果存在,求出实数a的值,若不存在,说明理由.
解:(1)∵f(x)=ax-lnx,f′(x)=1- =
= ,
,
∴当0<x<1时,f′(x)<0,此时f(x)单调递减;
当1<x<e时,f′(x)>0,此时f(x)单调递增.…(3分)
∴f(x)的极小值为f(1)=1.…(4分)
(2)∵f(x)的极小值为1,即f(x)在(0,e)上的最小值为1,
∴f(x)>0,f(x)min=1.…(6分)
令h(x)=g(x)+ =
= +
+ ,h′(x)=
,h′(x)= ,
,
当0<x≤e时,h′(x)>0,h(x)在x∈(0,e]上单调递增,
∴h(x)≤h(e)= +
+ <
< +
+ =1,…(9分)
=1,…(9分)
∴在(1)的条件下,f(x)>g(x)+ .…(10分)
.…(10分)
(3)假设存在实数a,使f(x)=ax-lnx,x∈[0,e]有最小值3,f′(x)=a- =
=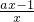 ,
,
①当0< <e时,f(x)在(0,
<e时,f(x)在(0, )上单调递减,在(
)上单调递减,在( ,e]上单调递增.
,e]上单调递增.
f(x)min=f( )=1+lna=3,a=e2,满足条件.…(13分)
)=1+lna=3,a=e2,满足条件.…(13分)
②当 ≥e时,f(x)在(0,e]上单调递减,f(x)min=f(e)=ae-1=3,a=
≥e时,f(x)在(0,e]上单调递减,f(x)min=f(e)=ae-1=3,a=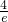 (舍去),
(舍去),
所以,此时f(x)无最小值.…(15分)
综上,存在实数a=e2,使得当x∈(0,e]时f(x)有最小值为3.…(16分)
分析:(1)先求导函数,由导数小于0得单调减区间,导数大于0的增区间,从而确定函数的极值;
(2)确定f(x)在(0,e)上的最小值为1,h(x)=g(x)+ 在(0,e]上的最大值为1,从而得证;
在(0,e]上的最大值为1,从而得证;
(3)假设存在实数a,使f(x)=ax-lnx,x∈[0,e]有最小值3,由于f′(x)=a- =
=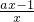 ,故要进行分类讨论:
,故要进行分类讨论:
①0< <e;②
<e;② ≥e,从而得解.
≥e,从而得解.
点评:本题以函数为载体,考查导数的运用,考查函数的极值,考查函数的最值,同时考查了存在性问题.
 =
= ,
,∴当0<x<1时,f′(x)<0,此时f(x)单调递减;
当1<x<e时,f′(x)>0,此时f(x)单调递增.…(3分)
∴f(x)的极小值为f(1)=1.…(4分)
(2)∵f(x)的极小值为1,即f(x)在(0,e)上的最小值为1,
∴f(x)>0,f(x)min=1.…(6分)
令h(x)=g(x)+
 =
= +
+ ,h′(x)=
,h′(x)= ,
,当0<x≤e时,h′(x)>0,h(x)在x∈(0,e]上单调递增,
∴h(x)≤h(e)=
 +
+ <
< +
+ =1,…(9分)
=1,…(9分)∴在(1)的条件下,f(x)>g(x)+
 .…(10分)
.…(10分)(3)假设存在实数a,使f(x)=ax-lnx,x∈[0,e]有最小值3,f′(x)=a-
 =
=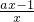 ,
,①当0<
 <e时,f(x)在(0,
<e时,f(x)在(0, )上单调递减,在(
)上单调递减,在( ,e]上单调递增.
,e]上单调递增.f(x)min=f(
 )=1+lna=3,a=e2,满足条件.…(13分)
)=1+lna=3,a=e2,满足条件.…(13分)②当
 ≥e时,f(x)在(0,e]上单调递减,f(x)min=f(e)=ae-1=3,a=
≥e时,f(x)在(0,e]上单调递减,f(x)min=f(e)=ae-1=3,a=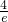 (舍去),
(舍去),所以,此时f(x)无最小值.…(15分)
综上,存在实数a=e2,使得当x∈(0,e]时f(x)有最小值为3.…(16分)
分析:(1)先求导函数,由导数小于0得单调减区间,导数大于0的增区间,从而确定函数的极值;
(2)确定f(x)在(0,e)上的最小值为1,h(x)=g(x)+
 在(0,e]上的最大值为1,从而得证;
在(0,e]上的最大值为1,从而得证;(3)假设存在实数a,使f(x)=ax-lnx,x∈[0,e]有最小值3,由于f′(x)=a-
 =
=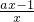 ,故要进行分类讨论:
,故要进行分类讨论:①0<
 <e;②
<e;② ≥e,从而得解.
≥e,从而得解.点评:本题以函数为载体,考查导数的运用,考查函数的极值,考查函数的最值,同时考查了存在性问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目