题目内容
已知定义域为R的函数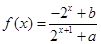
是奇函数。
⑴求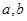
的值；并判定函数
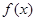单调性（不必证明）。
⑵若对于任意的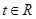
，不等式
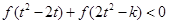恒成立，求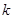
的取值范围。
【答案】
题：⑴可用
或两个特殊的值求出
，
，
∴
，可得
在
上为单调减函数；………6分
⑵由
得
，在上为单调减函数
∴有
在R上恒成立，只需
小于
的最小值，
而的最小值为
，所以
，（还可以用△
求解）。………12分
【解析】略
练习册系列答案
相关题目