题目内容
(文科做)数列{an}中,a3=1,Sn=an+1(n=1,2,3…).
(I)求a1,a2;
(II)求数列{an}的前n项和Sn;
(III)设bn=log2Sn,存在数列{cn}使得cn•bn+3•bn+4=1,试求数列{cn}的前n项和.
解:(I)∵a1=a2,a1+a2=a3,
∴2a1=a3=1,
∴ .…2分
.…2分
(II)∵Sn=an+1=Sn+1-Sn,
∴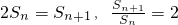 ,…6分
,…6分
∴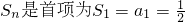 ,公比为2的等比数列.
,公比为2的等比数列.
∴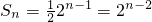 .(n∈N*).…9分
.(n∈N*).…9分
(III)∵bn=log2Sn,Sn=2n-2,
∴bn=n-2,bn+3=n+1,bn+4=n+2,
∴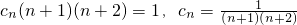 =
= .…11分
.…11分
∴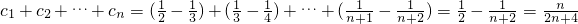 .…14分
.…14分
分析:(I)通过已知的关系式直接求a1,a2;
(II)利用an+1=Sn+1-Sn,与已知的关系式,推出数列{Sn}是等比数列,即可求数列{an}的前n项和Sn;
(III)设bn=log2Sn,求出bn的表达式,求出数列{cn}的通项公式,通过裂项法求数列{cn}的前n项和.
点评:本题是中档题,考查数列递推关系式的应用,数列通项公式的求法,前n项和的求法,考查计算能力,逻辑推理能力.
∴2a1=a3=1,
∴
 .…2分
.…2分(II)∵Sn=an+1=Sn+1-Sn,
∴
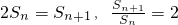 ,…6分
,…6分∴
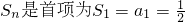 ,公比为2的等比数列.
,公比为2的等比数列.∴
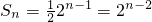 .(n∈N*).…9分
.(n∈N*).…9分(III)∵bn=log2Sn,Sn=2n-2,
∴bn=n-2,bn+3=n+1,bn+4=n+2,
∴
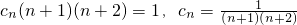 =
= .…11分
.…11分∴
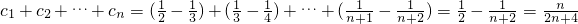 .…14分
.…14分分析:(I)通过已知的关系式直接求a1,a2;
(II)利用an+1=Sn+1-Sn,与已知的关系式,推出数列{Sn}是等比数列,即可求数列{an}的前n项和Sn;
(III)设bn=log2Sn,求出bn的表达式,求出数列{cn}的通项公式,通过裂项法求数列{cn}的前n项和.
点评:本题是中档题,考查数列递推关系式的应用,数列通项公式的求法,前n项和的求法,考查计算能力,逻辑推理能力.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
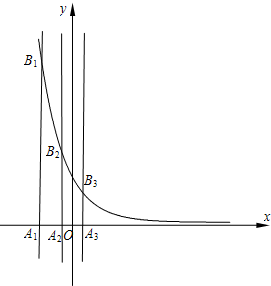 (2006•蚌埠二模)已知等差数列{an}的首项为p,公差为d(d>0).对于不同的自然数n,直线x=an与x轴和指数函数
(2006•蚌埠二模)已知等差数列{an}的首项为p,公差为d(d>0).对于不同的自然数n,直线x=an与x轴和指数函数 (文科做)已知点A1(2,0),A2(1,t),A3(0,b),A4(-1,t),A5(-2,0),其中t>0,b为正常数.
(文科做)已知点A1(2,0),A2(1,t),A3(0,b),A4(-1,t),A5(-2,0),其中t>0,b为正常数.