Question

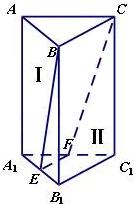正三棱柱ABC-A₁B₁C₁中，所有棱长均相等，E，F分别是棱A₁B₁，A₁C₁的中点，截面EBCF将三棱柱截成几何体Ⅰ和几何体Ⅱ两个几何体．
①求几何体Ⅰ和几何体Ⅱ的表面积之比；
②求几何体Ⅰ和几何体Ⅱ的体积之比．

Answer 1

分析：（1）易知几何体Ⅰ是一个三棱台，侧面积等于5个侧面面积的和，几何体Ⅱ也有5个面，侧面积等于5个侧面面积的和，将这两个几何体的表面积相除，可得结果．
（2） 几何体Ⅰ是一个三棱台，其体积由面积公式可求得；几何体Ⅱ的体积用整个三棱柱的体积减去几何体Ⅰ的体积可得，计算这两个几何体的体积之比．

解答：解：（1）设正三棱柱ABC-A₁B₁C₁中，所有棱长均为1，由三角形的中位线的性质得A₁EF的面积
为

1

4

×（

1

2

×1×1×

3

2

）=

3

16

，BE=

1+ 1 4

=

5

2

，
几何体Ⅰ的全面积为

3

16

+2×（

1+ 1 2

2

×1）+

1

2

×1×1×

3

2

+

(1+ 1 2 ) 5 4 - 1 16

2

=

5 3 +24+3 19

16

．
几何体Ⅱ的表面积为 1×1+2×（

1

2

×

1

2

×1）+

3

4

（

1

2

×1×1×

3

2

）+

(1+ 1 2 ) 5 4 - 1 16

2

=

24+3 3 +3 19

16

，
 故求几何体Ⅰ和几何体Ⅱ的表面积之比为：

5 3 +24+3 19

3 3 +24+3 19

．
（2） 几何体Ⅰ是一个三棱台，其体积为

1

3

×（

3

16

+

3 16 × 3 4

+

3

4

）×1=

7 3

48

，
几何体Ⅱ的体积为

3

4

×1-

7 3

48

=

5 3

48

，
故几何体Ⅰ和几何体Ⅱ的体积之比为：

7

5

．

点评：本题考查棱柱、棱台的表面积、体积的计算方法，以及用间接方法求出不规则几何体的体积．