题目内容
如图,已知椭圆 的离心率为
的离心率为 ,过椭圆右焦点
,过椭圆右焦点 作两条互相垂直的弦
作两条互相垂直的弦 与
与 ,当直线
,当直线 的斜率为0时,
的斜率为0时, .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)求 的取值范围。
的取值范围。

解:(Ⅰ)当直线 的斜率为0时,直线
的斜率为0时,直线 垂直于
垂直于 轴,
轴,

 ,
, ,即
,即 
 ,且
,且 ,解得:
,解得:
所以椭圆方程为 。…………………(6分)
。…………………(6分)
(Ⅱ)①当两条弦中一条斜率为0时,另一条弦的斜率不存在,
由题意可知, ;…………………(7分)
;…………………(7分)
②当两条弦斜率均存在且不为0时,设 ,
,
设直线 的方程为
的方程为 ,则直线
,则直线 的方程为
的方程为
将直线 的方程代入椭圆方程中,并整理得
的方程代入椭圆方程中,并整理得
 …………………(9分)
…………………(9分)
 ,
,
同理,
 …………………(11分)
…………………(11分)
令 ,则
,则
所以

 ,
,

所以
综合①②可知, 的取值范围为
的取值范围为 。…………………(14分)
。…………………(14分)

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 在直线
在直线 上,则
上,则 的最小值是__________。
的最小值是__________。
 的弧所对的圆心角为
的弧所对的圆心角为 ,则这条弧所在的扇形面积为
,则这条弧所在的扇形面积为  .
. 分别为双曲线
分别为双曲线 的左、右焦点,若在双曲线的右支上存在点P,满足
的左、右焦点,若在双曲线的右支上存在点P,满足 ,且原点O到直线
,且原点O到直线 的距离等于双曲线的实半轴长,则该双曲线的渐近线方程为( )
的距离等于双曲线的实半轴长,则该双曲线的渐近线方程为( ) B.
B. C.
C. D.
D.
 :
: 和圆
和圆 :
: ,倾斜角为
,倾斜角为 的直线
的直线 经过
经过 四点,则
四点,则 的值为
的值为 
 的准线的方程是
的准线的方程是 ,则实数a的值是( )
,则实数a的值是( ) C.
C.  D.
D. 
 是定义在非零实数集上的函数,
是定义在非零实数集上的函数, 时,
时, ,记
,记 ,则 ( )
,则 ( ) B.
B. C.
C. D.
D.
 ,
,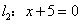 ,则直线
,则直线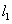 与
与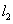 的夹角为= .
的夹角为= .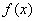 是定义在R上的偶函数,对任意
是定义在R上的偶函数,对任意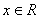 ,都有
,都有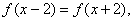 且当
且当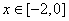 时,
时, .若在区间
.若在区间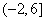 内关于
内关于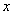 的方程
的方程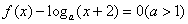 恰有3个不同的实数根,则实数
恰有3个不同的实数根,则实数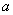 的取值范围是( )
的取值范围是( ) B.
B.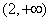 C.
C.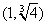 D.
D.