题目内容
设m、n为正整数,且m≠2,二次函数y=x2+(3-mt)x-3mt的图象与x轴的两个交点间的距离为的d1,二次函数y=-x2+(2t-n)x+2nt的图象与x轴的两个交点间的距离为d2,如果d1≥d2对一切实数t恒成立,求m、n的值.
【答案】分析:设二次函数y=x2+(3-mt)x-3m的图象与x轴的两个交点分别为(x1,0),(x2,0),二次函数y=-x2+(2t-n)x+2nt的图象与x轴的两个交点分别为(x3,0),(x4,0),则d1=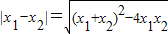 =
=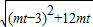 ,
,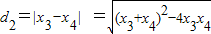 =
=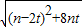 .由d1≥d2对一切实数t恒成立,知(m2-4)t2+(6m-4n)t+9-n2≥0对一切实数t恒成立,由此能求出m、n的值.
.由d1≥d2对一切实数t恒成立,知(m2-4)t2+(6m-4n)t+9-n2≥0对一切实数t恒成立,由此能求出m、n的值.
解答:解:设二次函数y=x2+(3-mt)x-3m的图象与x轴的两个交点分别为(x1,0),(x2,0),
二次函数y=-x2+(2t-n)x+2nt的图象与x轴的两个交点分别为(x3,0),(x4,0),
则d1=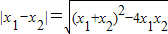
=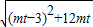 ,
,
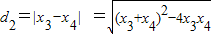
=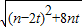 .
.
∵d1≥d2对一切实数t恒成立,
∴(mt-3)2+12mt≥(n-2t)2+8nt对一切实数t恒成立,
即(m2-4)t2+(6m-4n)t+9-n2≥0对一切实数t恒成立,
∴ ,
,
∴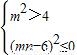 ,
,
又∵m、n为正整数,
∴m=3,n=2或m=6,n=1.…(14分)
点评:本题考查函数的恒成立问题,对数学思维的要求比较高,要求学生理解“存在”、“恒成立”,以及运用一般与特殊的关系进行否定,本题有一定的探索性.综合性强,难度大,易出错.
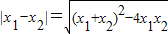 =
=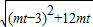 ,
,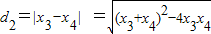 =
=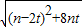 .由d1≥d2对一切实数t恒成立,知(m2-4)t2+(6m-4n)t+9-n2≥0对一切实数t恒成立,由此能求出m、n的值.
.由d1≥d2对一切实数t恒成立,知(m2-4)t2+(6m-4n)t+9-n2≥0对一切实数t恒成立,由此能求出m、n的值.解答:解:设二次函数y=x2+(3-mt)x-3m的图象与x轴的两个交点分别为(x1,0),(x2,0),
二次函数y=-x2+(2t-n)x+2nt的图象与x轴的两个交点分别为(x3,0),(x4,0),
则d1=
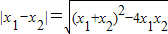
=
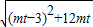 ,
,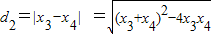
=
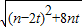 .
.∵d1≥d2对一切实数t恒成立,
∴(mt-3)2+12mt≥(n-2t)2+8nt对一切实数t恒成立,
即(m2-4)t2+(6m-4n)t+9-n2≥0对一切实数t恒成立,
∴
 ,
,∴
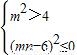 ,
,又∵m、n为正整数,
∴m=3,n=2或m=6,n=1.…(14分)
点评:本题考查函数的恒成立问题,对数学思维的要求比较高,要求学生理解“存在”、“恒成立”,以及运用一般与特殊的关系进行否定,本题有一定的探索性.综合性强,难度大,易出错.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目