题目内容
已知函数f(x)=(1+cotx)sin2x-2sin(x+ )sin(x-
)sin(x- ).
).
(1)若tanα=2,求f(α);
(2)若x∈[ ,
, ],求f(x)的取值范围.
],求f(x)的取值范围.
解:(1)∵f(x)=(1+cotx)sin2x-2sin(x+ )sin(x-
)sin(x- )=sin2x+sinxcosx+cos2x
)=sin2x+sinxcosx+cos2x
= +
+ =
=
∵tanα=2,∴sin2α=2sinαcosα= =
= =
= ,
,
cos2α= =
=
=
由tanα=2得 ,
,
 ,
,
所以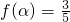 .
.
(2)由(1)得
由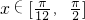 得
得 ,所以
,所以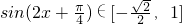
从而 .
.
分析:(1)利用正切化为正弦、余弦,利用两角和与差的三角函数展开,二倍角公式的应用化为 ,通过tanα=2,求出sin2α,cos2α,然后求出f(α);
,通过tanα=2,求出sin2α,cos2α,然后求出f(α);
(2)化简函数为: ,由x∈[
,由x∈[ ,
, ],求出2x+
],求出2x+ 的范围,然后求f(x)的取值范围.
的范围,然后求f(x)的取值范围.
点评:三角函数的化简,包括降幂扩角公式、辅助角公式都是高考考查的重点内容,另外对于三角函数的化简到最简形式一定要求掌握.熟练利用正余弦函数的图象求形如y=Asin(ωx+φ)性质.
 )sin(x-
)sin(x- )=sin2x+sinxcosx+cos2x
)=sin2x+sinxcosx+cos2x=
 +
+ =
=
∵tanα=2,∴sin2α=2sinαcosα=
 =
= =
= ,
,cos2α=
 =
=
=

由tanα=2得
 ,
, ,
,所以
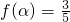 .
.(2)由(1)得

由
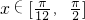 得
得 ,所以
,所以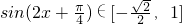
从而
 .
.分析:(1)利用正切化为正弦、余弦,利用两角和与差的三角函数展开,二倍角公式的应用化为
 ,通过tanα=2,求出sin2α,cos2α,然后求出f(α);
,通过tanα=2,求出sin2α,cos2α,然后求出f(α);(2)化简函数为:
 ,由x∈[
,由x∈[ ,
, ],求出2x+
],求出2x+ 的范围,然后求f(x)的取值范围.
的范围,然后求f(x)的取值范围.点评:三角函数的化简,包括降幂扩角公式、辅助角公式都是高考考查的重点内容,另外对于三角函数的化简到最简形式一定要求掌握.熟练利用正余弦函数的图象求形如y=Asin(ωx+φ)性质.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|