题目内容
(本小题满分12分)已知函数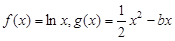 (
(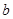 为常数)。
为常数)。
(Ⅰ)函数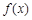 的图象在点(
的图象在点(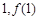 )处的切线与函数
)处的切线与函数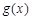 的图象相切,求实数
的图象相切,求实数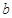 的值;
的值;
(Ⅱ)设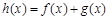 ,若函数
,若函数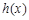 在定义域上存在单调减区间,求实数
在定义域上存在单调减区间,求实数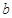 的取值范围;
的取值范围;
(Ⅲ)若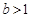 ,对于区间[1,2]内的任意两个不相等的实数
,对于区间[1,2]内的任意两个不相等的实数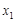 ,
,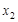 ,都有
,都有
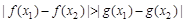 成立,求
成立,求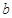 的取值范围。
的取值范围。
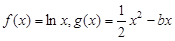 (
(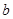 为常数)。
为常数)。(Ⅰ)函数
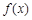 的图象在点(
的图象在点(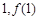 )处的切线与函数
)处的切线与函数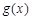 的图象相切,求实数
的图象相切,求实数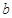 的值;
的值;(Ⅱ)设
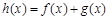 ,若函数
,若函数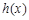 在定义域上存在单调减区间,求实数
在定义域上存在单调减区间,求实数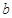 的取值范围;
的取值范围;(Ⅲ)若
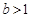 ,对于区间[1,2]内的任意两个不相等的实数
,对于区间[1,2]内的任意两个不相等的实数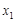 ,
,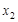 ,都有
,都有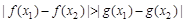 成立,求
成立,求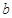 的取值范围。
的取值范围。(Ⅰ)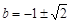 (Ⅱ)
(Ⅱ)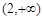 (Ⅲ)
(Ⅲ)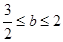
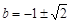 (Ⅱ)
(Ⅱ)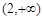 (Ⅲ)
(Ⅲ)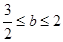
试题分析:(Ⅰ)因为
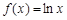 ,所以
,所以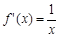 ,因此
,因此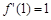 ,
,所以函数
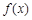 的图象在点(
的图象在点(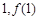 )处的切线方程为
)处的切线方程为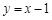 , ……1分
, ……1分由
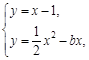 得
得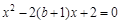 ,
,由
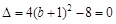 ,得
,得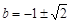 . ……3分
. ……3分(Ⅱ)因为
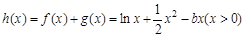 ,
,所以
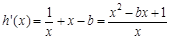 ,
,由题意知
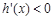 在
在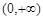 上有解,
上有解,因为
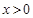 ,设
,设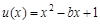 ,因为
,因为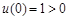 ,
,则只要
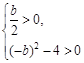 ,解得
,解得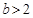 ,
,所以b的取值范围是
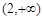 . ……6分
. ……6分(Ⅲ)不妨设
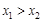 ,
,因为函数
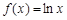 在区间[1,2]上是增函数,所以
在区间[1,2]上是增函数,所以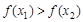 ,
,函数
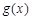 图象的对称轴为
图象的对称轴为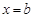 ,且
,且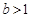 。
。(i)当
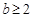 时,函数
时,函数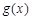 在区间[1,2]上是减函数,所以
在区间[1,2]上是减函数,所以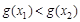 ,
,所以
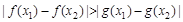 等价于
等价于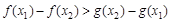 ,
,即
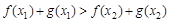 ,
,等价于
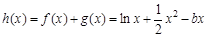 在区间[1,2]上是增函数,
在区间[1,2]上是增函数,等价于
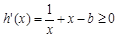 在区间[1,2]上恒成立,
在区间[1,2]上恒成立,等价于
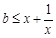 在区间[1,2]上恒成立,
在区间[1,2]上恒成立,所以
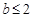 ,又
,又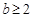 ,
,所以
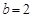 . ……8分
. ……8分(ii)当
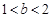 时,函数
时,函数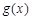 在区间[1, b]上是减函数,在
在区间[1, b]上是减函数,在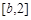 上为增函数。
上为增函数。① 当
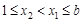 时,
时,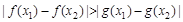 等价于
等价于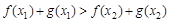 ,
,等价于
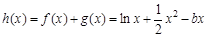 在区间[1,b]上是增函数,
在区间[1,b]上是增函数,等价于
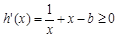 在区间[1,b]上恒成立,
在区间[1,b]上恒成立,等价于
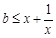 在区间[1,b]上恒成立,
在区间[1,b]上恒成立,所以
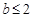 ,又
,又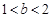 ,所以
,所以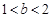
②当
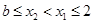 时,
时,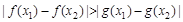 等价于
等价于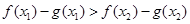 ,
,等价于
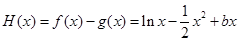 在区间[b,2]上是增函数,
在区间[b,2]上是增函数,等价于
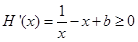 在区间[b,2]上恒成立,
在区间[b,2]上恒成立,等价于
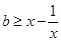 在区间[b,2]上恒成立,
在区间[b,2]上恒成立,所以
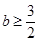 ,故
,故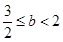 ,
,③当
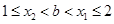 时,
时,由
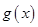 图像的对称性知,
图像的对称性知,只要
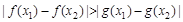 对于①②同时成立,
对于①②同时成立,那么对于③,则存在
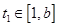 ,
,使
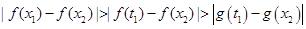 =
=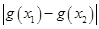 恒成立;
恒成立;或存在
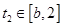 ,
,使
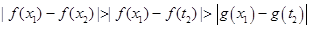 =
=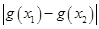 恒成立,
恒成立,因此
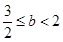 ,
, 综上,b的取值范围是
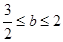 . ……12分
. ……12分点评:导数是研究函数的一个有力的工具,研究函数时,不要忘记考查函数的定义域.另外恒成立问题一般转化成求最值问题解决.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
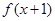 是定义在
是定义在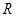 上的奇函数,若对于任意给定的不等实数
上的奇函数,若对于任意给定的不等实数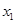 、
、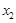 ,不等式
,不等式 恒成立,则不等式
恒成立,则不等式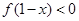 的解集为 .
的解集为 .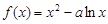 在
在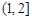 是增函数,
是增函数,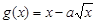 在(0,1)为减函数.
在(0,1)为减函数.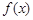 、
、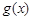 的表达式;
的表达式;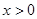 时,方程
时,方程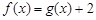 有唯一解;
有唯一解;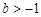 时,若
时,若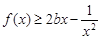 在
在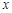 ∈
∈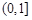 内恒成立,求
内恒成立,求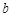 的取值范围.
的取值范围.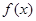 满足:x≥4,则
满足:x≥4,则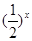 ;当x<4时
;当x<4时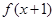 ,则
,则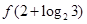 =
=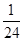
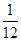
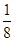
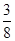
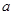 为非负实数,函数
为非负实数,函数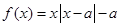 .
.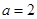 时,求函数的单调区间;
时,求函数的单调区间;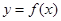 的零点个数,并求出零点.
的零点个数,并求出零点.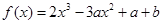 (其中a,b为实常数)。
(其中a,b为实常数)。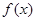 的单调区间:
的单调区间: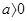 时,函数
时,函数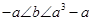 :
: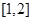 上是减函数,设关于x的方程
上是减函数,设关于x的方程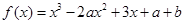 的两个非零实数根为
的两个非零实数根为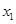 ,
,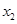 。试问是否存在实数m,使得
。试问是否存在实数m,使得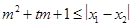 对任意满足条件的a及t
对任意满足条件的a及t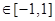 恒成立?若存在,求m的取值范围;若不存在,请说明理由。
恒成立?若存在,求m的取值范围;若不存在,请说明理由。 ,则实数
,则实数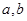 的大小顺序(从小到大)是 .
的大小顺序(从小到大)是 . ,则函数
,则函数 的定义域为 ____________;
的定义域为 ____________; (x>2)的最小值是( )
(x>2)的最小值是( )