题目内容

如图，直三棱柱ABC-A1B1C1中，AB=AC=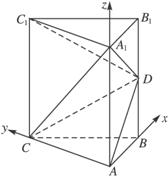AA1，∠BAC=90°，D为棱BB1的中点.

(1)求异面直线C1D与A1C所成的角;

(2)求证:平面A1DC⊥平面ADC.

解法一：（1）解析：建立如图所示的平面直角坐标系.

设AB=a,

则A1（0，0，2a），C（0，a，0），?C1（0，a，2a），D（a，0，a），

于是=（a,-a,-a）,=(0,a,-2a).

∵cos〈，〉=，

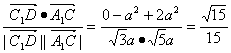∴异面直线C1D与A1C所成的角为arccos.

（2）证明：∵=（a,0,-a）,=(a,0,a),=(0,a,0),

∴·=a2+0-a2=0, ·=0.

则⊥，⊥.

∴A1D⊥平面ADC.又A1D平面A1DC，

∴平面A1DC⊥平面ADC.

解法二：（1）解析：连结AC1交A1C于点E，取AD中点F，连结EF，则EF∥C1D.

∴直线EF与A1C所成的角就是异面直线C1D与A1C所成的角.

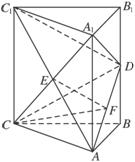
设AB=a，则C1D=a，

A1C=a，

AD=a.

△CEF中,CE=A1C=a,EF=C1D=a.

直三棱柱中，∠BAC=90°，则AD⊥AC.

CF=a.

∵cosCEF=.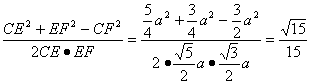

∴异面直线C1D与A1C所成的角为arccos.

（2）证明：直三棱柱中，∠BAC=90°，

∴AC⊥平面ABB1A1，则AC⊥A1D.

又AD=a,A1D=a,AA1=2a,

则AD2+A1D2=AA12，于是AD⊥A1D.

∴A1D⊥平面ADC.又A1D平面A1DC，∴平面A1DC⊥平面ADC.


练习册系列答案
相关题目
精英家教网如图，直三棱柱ABC-A1B1C1中，∠ACB=90°，AC=1，CB=
2
，侧棱AA1=1，侧面AA1B1B的两条对角线交于点D，B1C1的中点为M，求证：CD⊥平面BDM．
精英家教网如图，直三棱柱ABC-A1B1C1中，底面是以∠ABC为直角的等腰直角三角形，AC=2a，BB1=3a，D为A1C1的中点，E为B1C的中点．
（1）求直线BE与A1C所成的角；
（2）在线段AA1中上是否存在点F，使CF⊥平面B1DF，若存在，求出|
AF
|；若不存在，说明理由．
精英家教网如图在直三棱柱ABC-A1B1C1中∠ACB=90°，AA1=2，AC=BC=1，则异面直线A1B与AC所成角的余弦值是
 
．
如图，直三棱柱ABC-A1B1C1中，AC⊥BC，AC=BC=CC1=2，M，N分别为AC，B1C1的中点．
（Ⅰ）求线段MN的长；
（Ⅱ）求证：MN∥平面ABB1A1；
（Ⅲ）线段CC1上是否存在点Q，使A1B⊥平面MNQ？说明理由．
精英家教网如图，直三棱柱ABC-A1B1C1中，∠BAC=90°，AB=AC=a，AA1=2a，D棱B1B的中点．
（Ⅰ）证明：A1C1∥平面ACD；
（Ⅱ）求异面直线AC与A1D所成角的大小；
（Ⅲ）证明：直线A1D⊥平面ADC．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网